filmov
tv
An Easy Exponential Equation | Stanford Mathematics Tournament
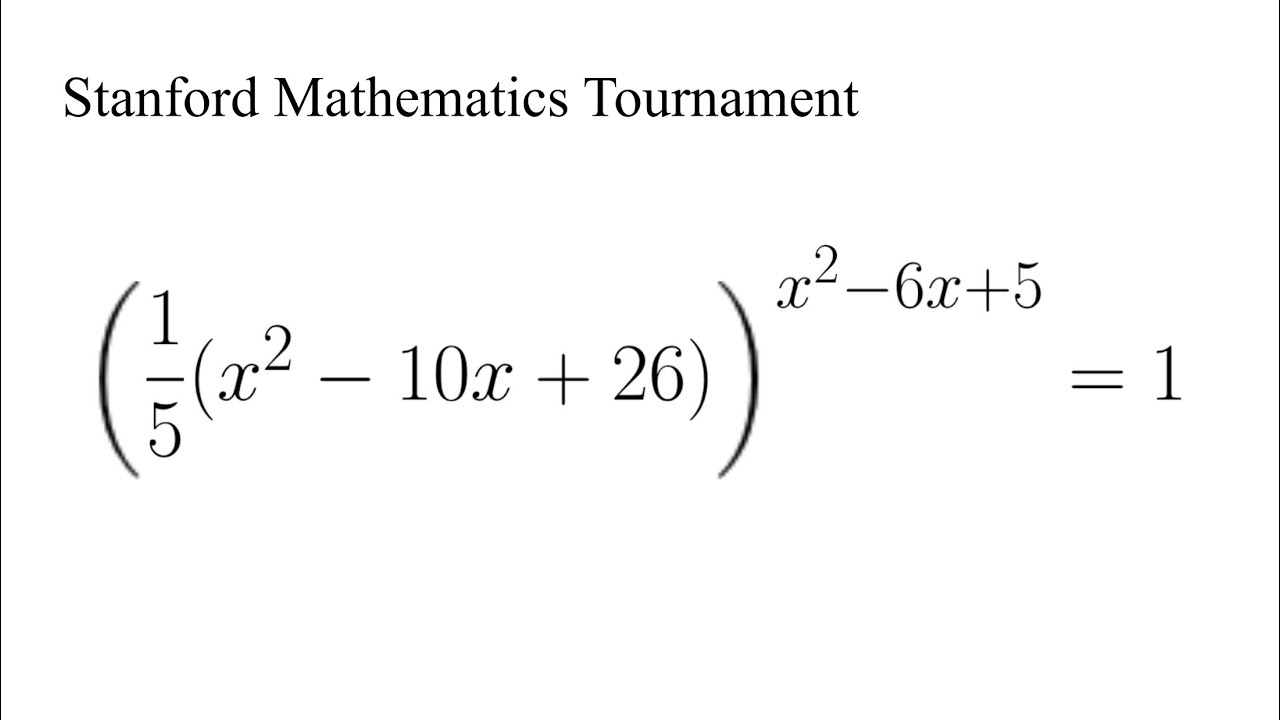
Показать описание
Solving Exponential Equations
Exponential Equations - Algebra and Precalculus
Solving Exponential Equation
Exponential Equation Grade 10
Introduction to Exponential Functions - Nerdstudy
Nice and Easy | Exponential Equations | Exponential Problems.
How to solve an exponential equation (without logarithm)
Solving A Quick and Easy Exponential Equation
A Trending Math Olympiad Exponential Equation.
Solving Exponential and Logarithmic Equations
How to Solve Exponential Equations using Logarithms - No Common Base Present
Can you solve this? | Exponential Equation | Algebra Problem.
Understanding Exponential Functions and their Gradients: Intuitive Approach
How to solve exponential equations (10 examples from easy to hard!)
SOLVING EXPONENTIAL EQUATIONS |jensenmath.ca|
How do you solve an exponential equation with e as the base
A Quick And Easy Exponential Equation
Exponential growth functions | Exponential and logarithmic functions | Algebra II | Khan Academy
Solving Exponential Equation @KasyannoEZMath
Exponential Equations - College Algebra
LAWS OF EXPONENTS | MATHS TRICKS
A Nice Math Olympiad Exponential Equation 3^x = X^9
Solving Exponential Equations Using Logarithms & The Quadratic Formula
Can You Solve this Exponential Equation? | Easy Step-by-Step Tutorial
Комментарии
 0:16:36
0:16:36
 0:05:58
0:05:58
 0:00:56
0:00:56
 0:01:39
0:01:39
 0:03:22
0:03:22
 0:05:25
0:05:25
 0:00:44
0:00:44
 0:00:28
0:00:28
 0:05:45
0:05:45
 0:07:08
0:07:08
 0:05:47
0:05:47
 0:03:33
0:03:33
 0:08:10
0:08:10
 0:33:03
0:33:03
 0:06:18
0:06:18
 0:02:47
0:02:47
 0:00:34
0:00:34
 0:07:41
0:07:41
 0:00:59
0:00:59
 0:11:52
0:11:52
 0:00:42
0:00:42
 0:02:34
0:02:34
 0:11:05
0:11:05
 0:09:29
0:09:29