filmov
tv
Hardest maths questions: simultaneous diophantine equations
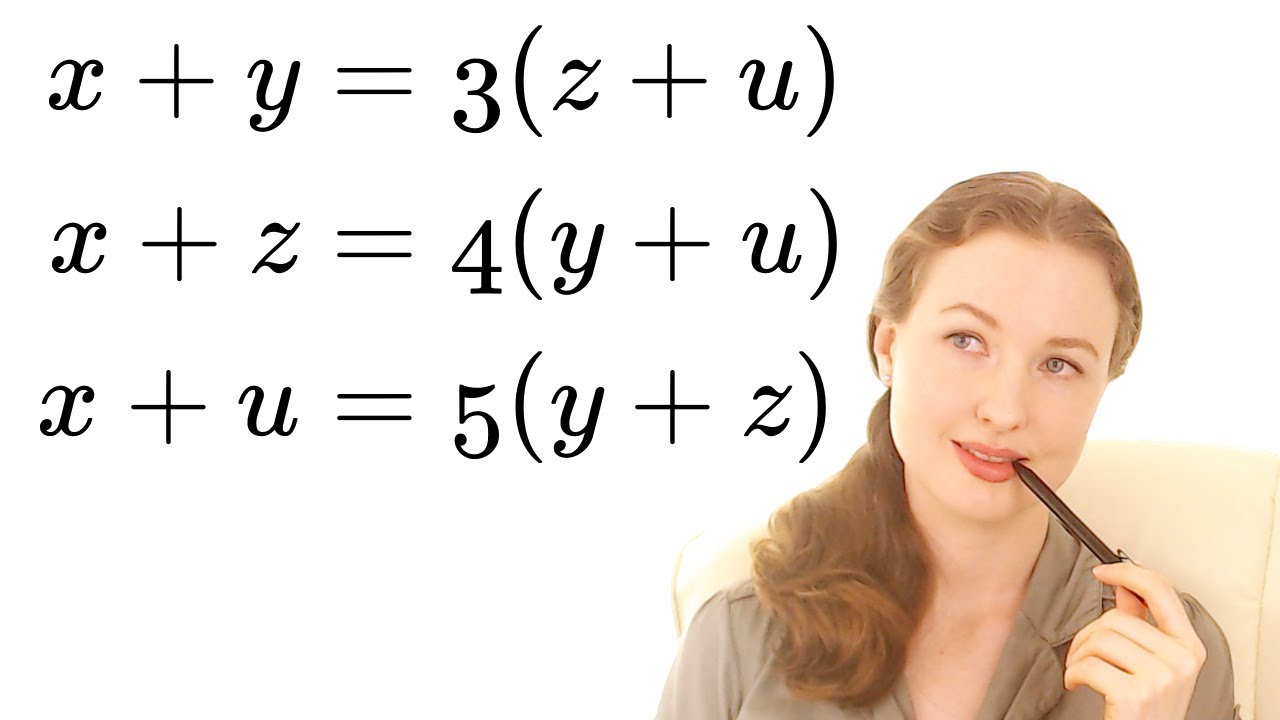
Показать описание
This question from the 2007 Australian Mathematics Competition (senior division) involves 3 simultaneous equations with positive integer solutions. We have to find the smallest value that x can take. 0% of students got this one right! I'll be making heavy use of the elimination method in this video, although you could use substitution instead.
Hardest maths questions: simultaneous diophantine equations
5 simple unsolvable equations
When mathematicians get bored (ep1)
Hardest math questions: |x| + |y| + |x+y| ≤ 2, area = ?
Math Olympiad Problem - Diophantine Equation
A Tough Diophantine Equation!
521 Math #22: Diophantine Equation
THE HARDEST MATHS EQUATION SOLVED!
Hardest maths questions - minimisation
Hardest maths questions - find a^4 + b^4 + c^4
Finding Integer Solutions | Math Olympiad Question
Hardest algebra question ever maths
This is How We Usually Solve Diophantine Equations In Math Olympiads
A Hyperbolic Diophantine Equation
Hardest Maths Questions (Junior) - Candles
Solution 62: Cleverly Manipulating a Diophantine Equation with x^2018
A system of diophantine equations | feat. Fermat's Last Theorem | must watch till the end
Number Theory | Linear Diophantine Equations
Quadratic Equations IIT Questions No 11 ( X Class)
Quadratic Diophantine Contradicitions
A Nice Math Olympiad Question. You Should Be Able Solve this Problem
Math Olympiad 3^m–2^m=65 | Math Olympiad Problems | Algebra
Hardest maths questions - tyres
Harder simultaneous equations questions
Комментарии
 0:10:25
0:10:25
 0:00:50
0:00:50
 0:00:37
0:00:37
 0:07:09
0:07:09
 0:04:10
0:04:10
 0:09:52
0:09:52
 0:04:14
0:04:14
 0:00:50
0:00:50
 0:10:27
0:10:27
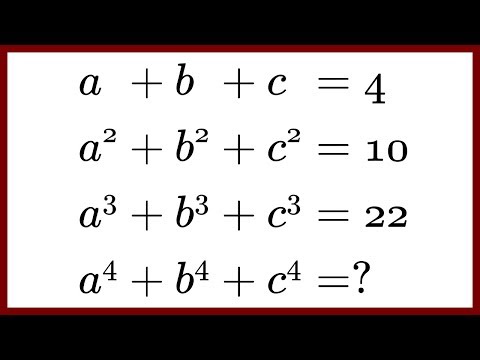 0:12:23
0:12:23
 0:08:18
0:08:18
 0:00:26
0:00:26
 0:03:33
0:03:33
 0:04:52
0:04:52
 0:07:45
0:07:45
 0:07:42
0:07:42
 0:02:25
0:02:25
 0:09:17
0:09:17
 0:00:50
0:00:50
 0:05:13
0:05:13
 0:04:05
0:04:05
 0:10:49
0:10:49
 0:06:59
0:06:59
 0:12:12
0:12:12