filmov
tv
Russian Math Olympiad Problem | A Very Nice Geometry Challenge

Показать описание
Russian Math Olympiad Question
Russian Math Olympiad | Best Geometry Problems
Russia | Math Olympiad Question | You should know this trick!!
Russian Maths Olympiads
Russian l can you solve this?? l Nice Olympiad Exponential Problem l Calculator not Allowed
Ukraine l Very Nice Olympiad Math Radical Problem l m=?
Russian Math Olympiad Problem | A Very Nice Geometry Challenge
Russian Math Olympiad Question
Russian Math Olympiad Problem | A Very Nice Geometry Challenge
Day 2 All-Russian Math Olympiad 2013 | Discrete Mathematics | Math Olympiad Training
A Nice Diophantine Equation from Russian Math Olympiad with Interesting Skills You Should Know
Russian | You should know this | Math Olympiad Trick
Russian- Math Olympiad Question International Maths Olympiad Problem | Find Value of X
Russian Maths Olympiad 1996 Q4 | Math Olympiad Training
A difficult olympiad math problem | China Math Olympiad Questions
Russian Math Olympiad | A Very Nice Geometry Problem
Russian Math Olympiad Question | How to solve this
Russian Math Olympiad | A Very Nice Geometry Problem | Find the area of the square
Russian l Hard Exponential Olympiad Math Problem l find value of x=?
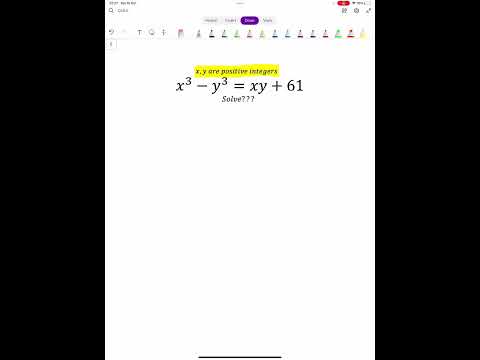
Find all integer solutions (Russian Math Olympiad)
Russian Maths Olympiad Problem I SAT I MCAT I Xth I GRE I Pre-Math I NSO | IMO | SOF
Russian Math Olympiad Question
Russian Math Olympiad Question #infinitypimath
Russian l can you solve this exponential problem?? l Olympiad Mathematics
Комментарии
 0:03:42
0:03:42
 0:09:58
0:09:58
 0:08:01
0:08:01
 0:00:12
0:00:12
 0:15:43
0:15:43
 0:16:04
0:16:04
 0:19:38
0:19:38
 0:01:35
0:01:35
 1:15:18
1:15:18
 0:01:11
0:01:11
 0:08:26
0:08:26
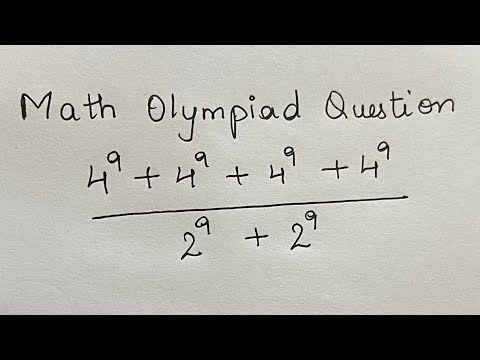 0:01:26
0:01:26
 0:04:31
0:04:31
 0:06:41
0:06:41
 0:11:39
0:11:39
 0:14:34
0:14:34
 0:02:12
0:02:12
 0:13:23
0:13:23
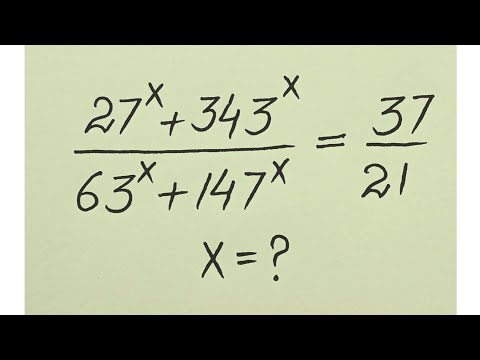 0:16:21
0:16:21
 0:20:56
0:20:56
 0:14:32
0:14:32
 0:04:22
0:04:22
 0:01:00
0:01:00
 0:15:12
0:15:12