filmov
tv
Solving Rational Inequalities Practice Test Full Solutions
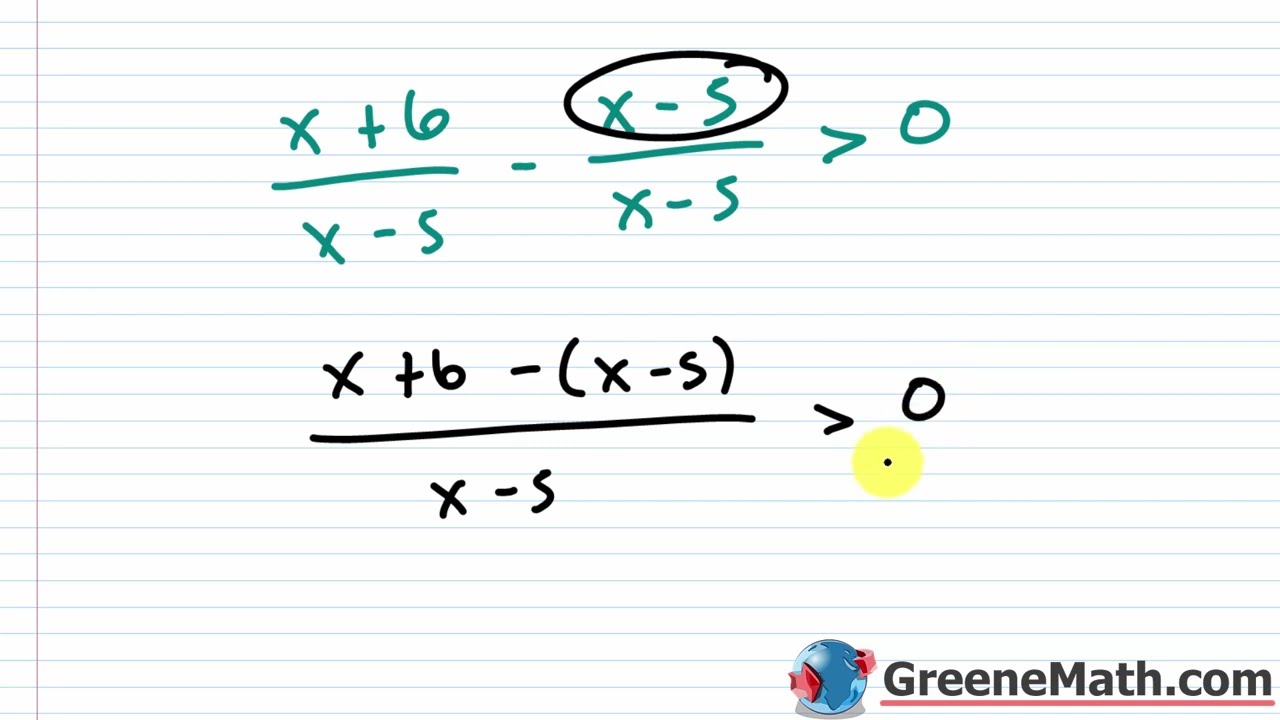
Показать описание
Step-by-Step full solutions for our practice test on solving rational inequalities. The process here involves obtaining a single rational expression on the left side and zero on the right. From there, we will set the numerator equal to zero and solve the resulting equation. Next, we will set the denominator equal to zero and solve the resulting equation. These solutions give us the critical values which are used to set up intervals on the number line. We can then test inside of these intervals to obtain our solution. Lastly, we will consider our critical values separately. Any values that create a zero denominator will be rejected while values that create a zero numerator will be kept if we have a non-strict inequality or rejected with a strict inequality.
Chapters:
0:00 Problem #1
6:49 Problem #2
9:57 Problem #3
12:47 Problem #4
22:08 Problem #5
30:57 Problem #6
35:51 Problem #7
43:07 Problem #8
51:18 Problem #9
55:22 Problem #10
 0:59:45
0:59:45
 0:10:18
0:10:18
 0:06:44
0:06:44
 0:08:35
0:08:35
 0:14:04
0:14:04
 1:03:16
1:03:16
 0:03:24
0:03:24
 0:10:11
0:10:11
 0:14:08
0:14:08
 0:13:19
0:13:19
 0:50:36
0:50:36
 0:37:39
0:37:39
 0:08:16
0:08:16
 0:07:49
0:07:49
 0:28:07
0:28:07
 0:15:20
0:15:20
 0:07:30
0:07:30
 0:02:56
0:02:56
 0:25:32
0:25:32
 0:44:55
0:44:55
 0:13:45
0:13:45
 0:04:37
0:04:37
 0:20:41
0:20:41
 0:00:27
0:00:27