filmov
tv
An Infinite Radical Solved in Two Ways
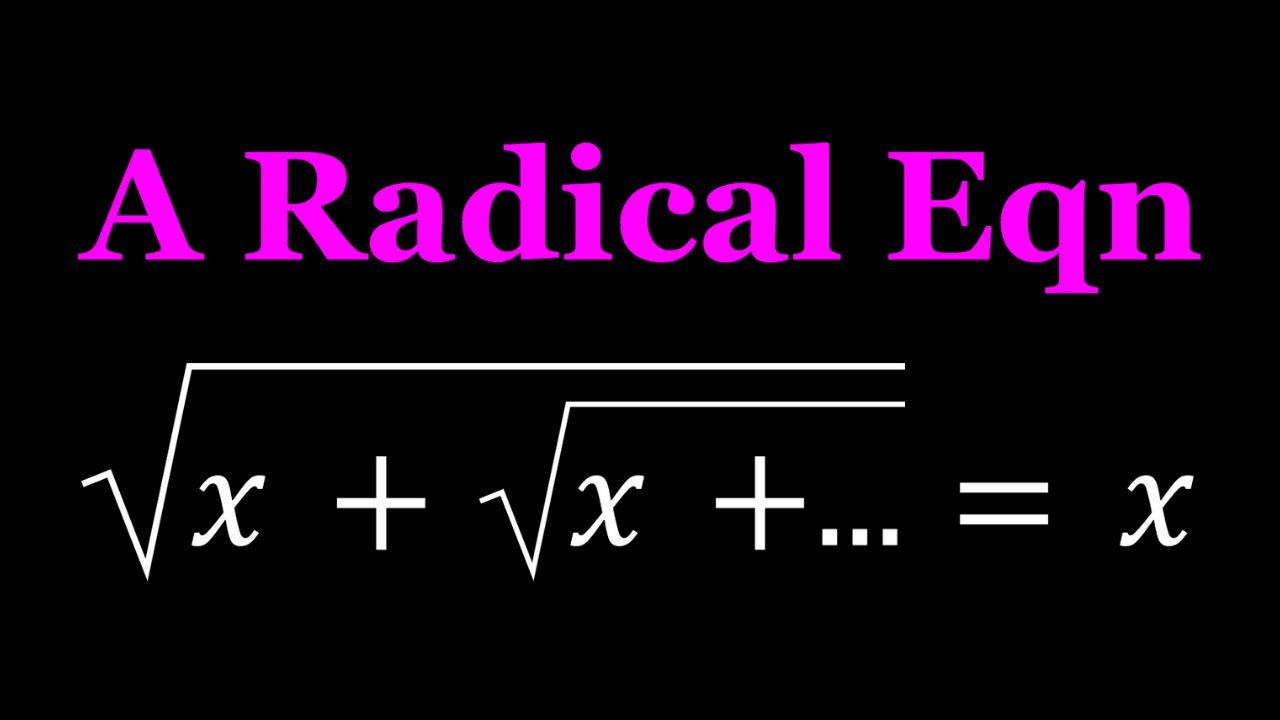
Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #RadicalEquations
PLAYLISTS 🎵 :
#ChallengingMathProblems #RadicalEquations
PLAYLISTS 🎵 :
An Infinite Radical Solved in Two Ways
An Infinite Radical Equation
Quickly Solving Infinite Radical Equations#mahs #radicals
Can You Solve This? Infinite Radicals
Solving an Infinite Radical Equation in Two Ways
In Seconds Solving Infinite Radical Equations#mahs #radicals #infinite
Infinite nested radicals
A nice infinite radical problem
Germany | A Nice Radical Math Simplification | Math Olympiad #maths #algebra #education #math
An Infinite Radical With A Special Flavor
(Putnam 1953) infinite nested radicals problem and the general case
Simplifying an Infinite Radical
An Infinite Radical with 3 and 2
Solving A Homemade Infinite Radical Equation
An Alternating Infinite Radical
An Infinite Series Under The Radical
Let's Solve An Infinite Radical Equation
Infinite Nested Radical
Solving An Infinite Radical for x
Simplifying An Infinite Radical Expression
Interesting trick to solve an interesting problem on infinite nested radical
An Infinite Radical Expression
An Infinite Radical | Algebra Challenge
An Infinite Radical Expression... | Math Olympiads
Комментарии
 0:08:48
0:08:48
 0:04:29
0:04:29
 0:00:31
0:00:31
 0:08:00
0:08:00
 0:08:41
0:08:41
 0:00:30
0:00:30
 0:06:18
0:06:18
 0:03:35
0:03:35
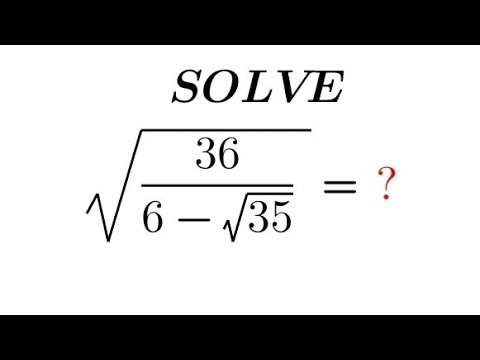 0:06:06
0:06:06
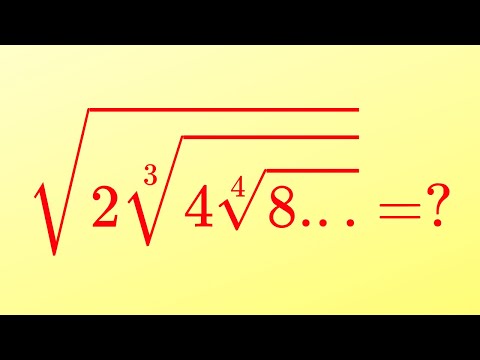 0:08:24
0:08:24
 0:09:31
0:09:31
 0:00:45
0:00:45
 0:05:10
0:05:10
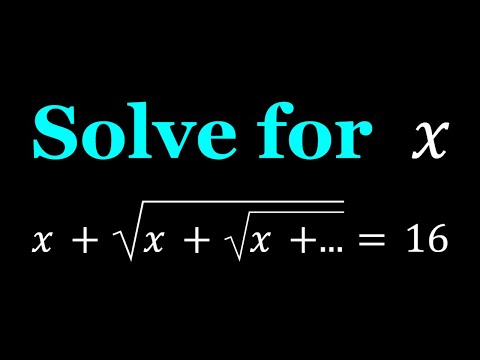 0:09:21
0:09:21
 0:10:19
0:10:19
 0:09:42
0:09:42
 0:08:14
0:08:14
 0:03:55
0:03:55
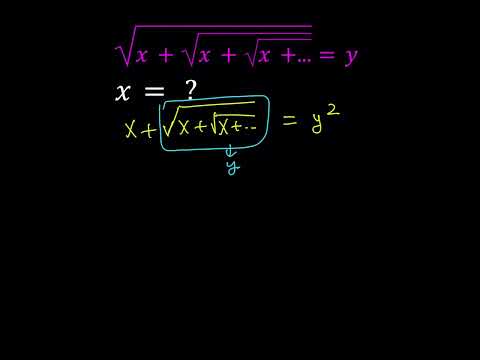 0:00:38
0:00:38
 0:08:48
0:08:48
 0:03:42
0:03:42
 0:00:29
0:00:29
 0:00:39
0:00:39
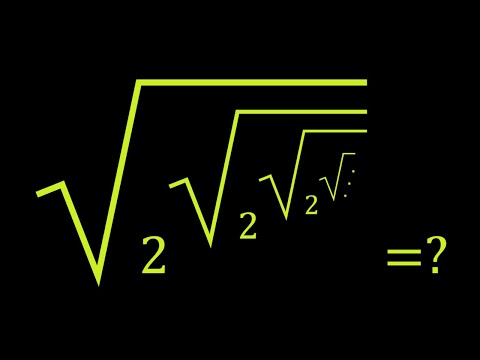 0:11:11
0:11:11