filmov
tv
Example of Gram-Schmidt Orthogonalization
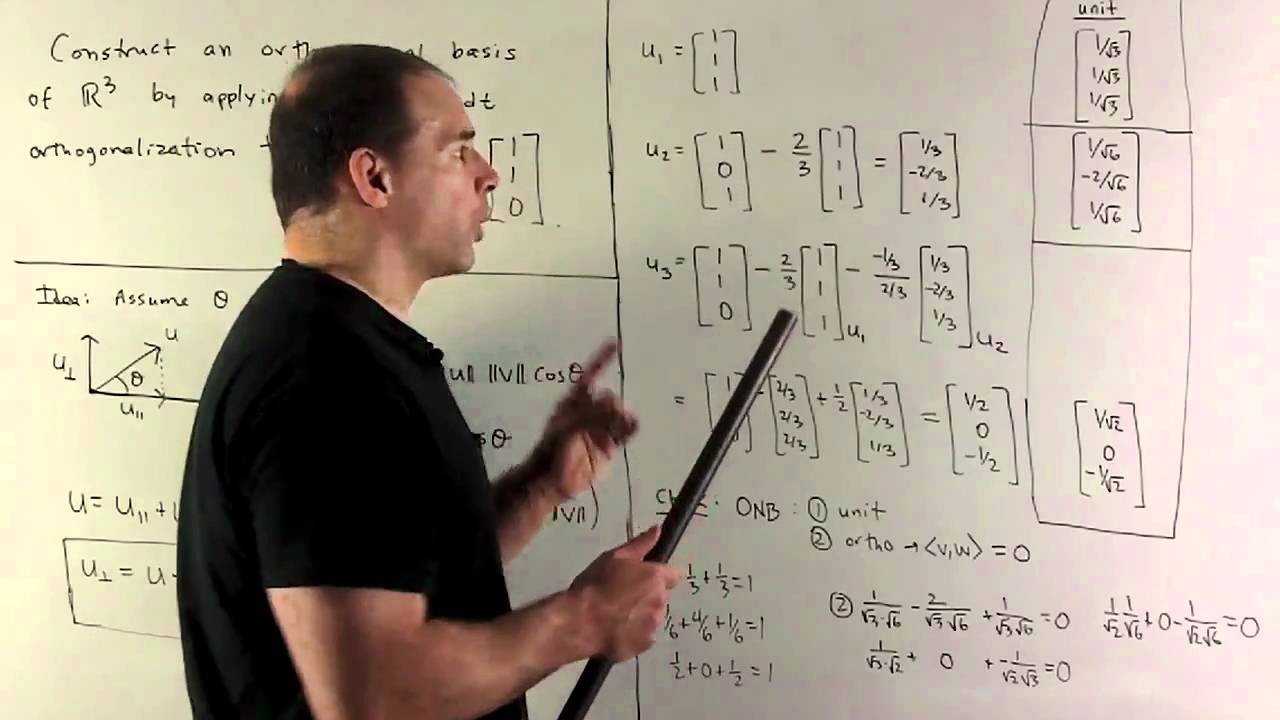
Показать описание
Linear Algebra: Construct an orthonormal basis of R^3 by applying the Gram-Schmidt orthogonalization process to (1, 1, 1), (1, 0, 1), and (1, 1, 0). In addition, we show how the Gram-Schmidt equations allow one to factor an invertible matrix into an orthogonal matrix times an upper triangular matrix.
Full example: using Gram-Schmidt
Example of Gram-Schmidt Orthogonalization
The Gram-Schmidt Process
Gram-Schmidt Orthogonalization (Proof and Example) | Linear Algebra
Gram-Schmidt Orthogonalization
Example on Gram Schmidt Orthogonalization Process
An example of Gram-Schmidt Orthogonalization
Gram Schmidt Method, Orthogonal and Orhonormal Basis Example
Gram-Schmidt Orthogonalization
Gram Schmidt example
Gram-Schmidt example with 3 basis vectors | Linear Algebra | Khan Academy
Example - Gram-Schmidt Orthogonalization
Use the Gram-Schmidt process to find an orthonormal basis
3.8. Gram Schmidt orthogonalization procedure - An example
The Gram Schmidt Orthogonalisation Process: A Mathematical Explanation.
Digital Communication lecture 1.7.8
MORE EXAMPLES OF GRAM-SCHMIDT PROCESS
Gram Schmidt Orthogonalization Process examples
Linear Algebra: Gram-Schmidt
Gram-Schmidt Orthogonalization Procedure Example
6.2 Gram-Schmidt Orthogonalization Procedure
The Gram-Schmidt process | Alternate coordinate systems (bases) | Linear Algebra | Khan Academy
Linear Algebra - Lecture 40 - The Gram-Schmidt Process
Gram-Schmidt process example | Alternate coordinate systems (bases) | Linear Algebra | Khan Academy
Комментарии
 0:06:18
0:06:18
 0:09:52
0:09:52
 0:10:07
0:10:07
 0:15:21
0:15:21
 0:06:37
0:06:37
 0:13:00
0:13:00
 0:06:07
0:06:07
 0:05:55
0:05:55
 0:10:00
0:10:00
 0:07:09
0:07:09
 0:13:57
0:13:57
 0:08:51
0:08:51
 0:07:45
0:07:45
 0:07:00
0:07:00
 0:12:00
0:12:00
 0:05:06
0:05:06
 0:12:41
0:12:41
 0:06:03
0:06:03
 0:13:53
0:13:53
 0:36:32
0:36:32
 0:13:29
0:13:29
 0:19:24
0:19:24
 0:05:46
0:05:46
 0:13:14
0:13:14