filmov
tv
Use the Gram-Schmidt process to find an orthonormal basis
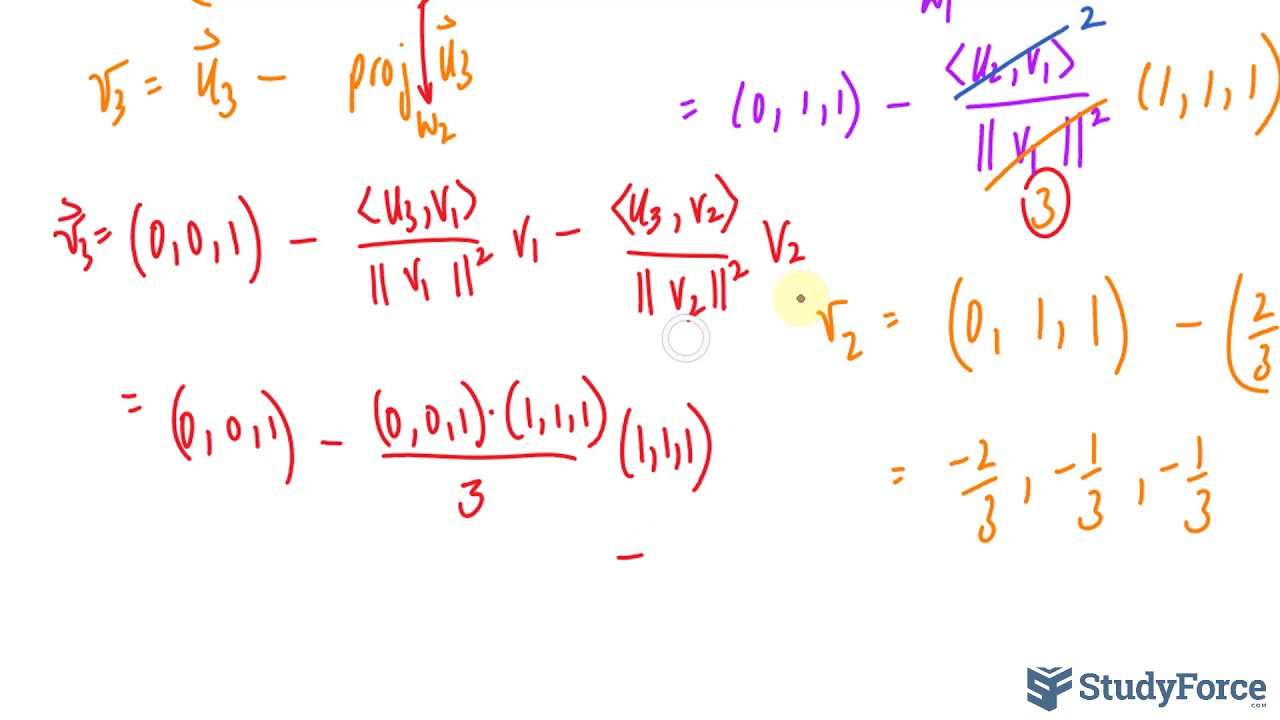
Показать описание
Follow us:
Q. Let S={u_1,u_2,u_3 } with the vectors defined below. S is a basis for R3. Use the Gram-Schmidt process to get an orthonormal basis.
u_1=(1,1,1) u_2=(0,1,1) u_3=(0,0,1)
Every nonzero finite-dimensional inner product space has an orthogonal basis.
#Orthonormal #LinearAlgebra #Projection
0:10:07
The Gram-Schmidt Process
0:06:18
Full example: using Gram-Schmidt
0:07:45
Use the Gram-Schmidt process to find an orthonormal basis
0:06:37
Gram-Schmidt Orthogonalization
0:05:46
Linear Algebra - Lecture 40 - The Gram-Schmidt Process
0:19:24
The Gram-Schmidt process | Alternate coordinate systems (bases) | Linear Algebra | Khan Academy
0:04:57
Gram-Schmidt procedure for obtaining orthonormal basis
0:13:44
Gram-Schmidt process | Lecture 19 | Matrix Algebra for Engineers
0:10:14
416.3B Using the Gram-Schmidt Process to Orthonormalize
0:13:53
Linear Algebra: Gram-Schmidt
0:32:31
Oxford Linear Algebra: Gram-Schmidt Process
0:20:34
Gram-Schmidt Orthogonalisation Process | Linear Algebra by GP Sir
0:10:44
Gram Schmidt Method Problem 1 - Vector Spaces - Engineering Mathematics - 4
0:12:00
The Gram Schmidt Orthogonalisation Process: A Mathematical Explanation.
0:04:33
QR Decomposition by The Gram-Schmidt Process - Linear Algebra
0:09:11
Using the Gram Schmidt process to find an orthogonal set of polynomials (Linear Algebra)
0:00:33
Use the Gram-Schmidt orthonormalization process to transform the given basis for R^n into an orth…
0:05:06
Digital Communication lecture 1.7.8
0:00:33
Use the Gram-Schmidt process to determine an orthonormal basis for the subspace of ℝ^n s…
0:09:45
Gram-Schmidt process example | Lecture 20 | Matrix Algebra for Engineers
0:00:33
Use the Gram-Schmidt process to transform the basis for the subspace W of Euclidean space R^3 into:…...
0:03:38
Linear Algebra: Gram-Schmidt Process (2 vectors)
0:14:46
Gram Schmidt process for QR decomposition using Python
0:10:11
Gram-Schmidt process
Комментарии