Discrete Math - 9.3.1 Matrix Representations of Relations and Properties

How to represent a relation using a matrix and easy tips for determining if the relation is reflexive, irreflexive, symmetric, antisymetric, asymmetric and transitive. Matrix operations are also reviewed (meet, join and Boolean product).

Video Chapters:
Introduction 0:00
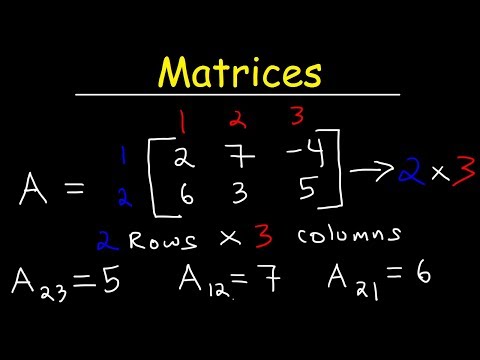
Matrix Representations 0:12
Matrix Representations in Reverse 3:09
Reflective Property 4:35
Irreflective Property 5:54
Symmetric Property 6:21
Anti-Symmetric Property 7:20
Asymmetric Property 8:34
Operations on Matrices 9:04
Transitive Property 15:55
Check for Understanding 17:00
Up Next 20:57

Textbook: Rosen, Discrete Mathematics and Its Applications, 7e

[ARSH]

This is by far the best video i watched explaining composite relations.
Miss i just wanted to say i owe you my degree.Thanks so much!

[pedro.balbino]

I'm here from the older video of the same topic. You're awesome !

[chocoopie]

thank you so much you clear my concept. you r good than my teacher

[jaydeestrada]

Can you clarify what you mean @8:33 when you say (1, 3) or (3, 1) are in the relationship but not both... how does that relate to what you wrote in green which states this means that mij = 0 or mji = 0, or both?

[jeroen]

Thank you for this video, I got stuck with composite relations and your video helped me understand it :>

[hindj]

What if I have a one in the original matrix that doesn’t occur in the product matrix but all ones in the product matrix match the ones is the original, does that make it not transitive?

[junaidmughal]

Love your videos, thanks alot Prof Brehm!

[nabeelfarooq]

Ma'am at 14:20 you say about squaring S but in the green color you have written square of matrix g. Please clarify.

[junaidmughal]

Also love your neat and colorful handwriting

[yasernimreh]

What about the transitive in the zero one matrix?

[outhide]

Lol leaving a comment on every video i hit today❤🤟💯