filmov
tv
Evaluate for theta between 0 and 2pi
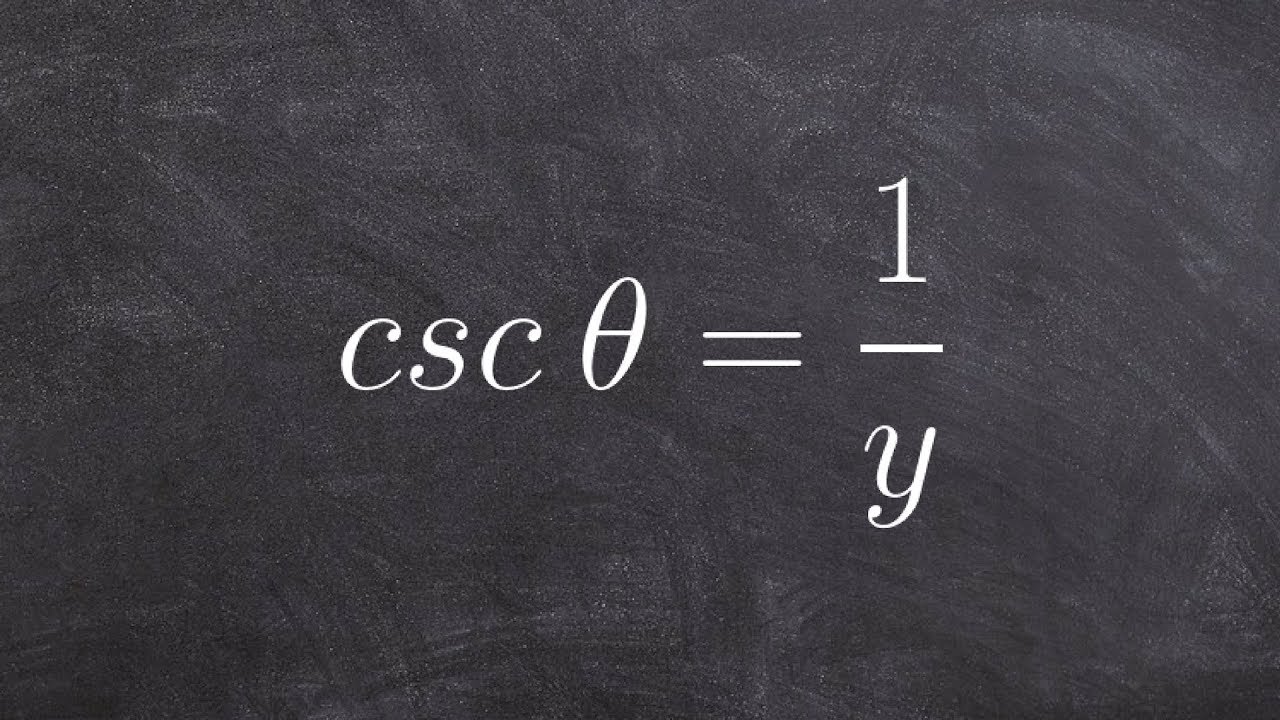
Показать описание
Learn how to solve trigonometric function problems using the unit circle. The trigonometric functions of an angle is the value of the trigonometric functions of sine, cosine, tangent, cosecant, secant and cotangent of that angle.
To use the unit circle in evaluating the trigonometric functions equations where the angle is unknown, we use the SOHCAHTOA principle to identify the point on the unit circle satisfying the value of the trigonometric function given. Then we can estimate the angle using our knowledge of the angles on a unit circle.
Recall that the x-coordinate of the coordinates of the terminal point formed by the angle on the unit circle represent the adjacent side of the triangle formed by the terminal side of an angle on a unit circle while the y-coordinate represent the opposite side of the triangle.
#trigonometry #unitcircle
#trigonometry #unitcircle
To use the unit circle in evaluating the trigonometric functions equations where the angle is unknown, we use the SOHCAHTOA principle to identify the point on the unit circle satisfying the value of the trigonometric function given. Then we can estimate the angle using our knowledge of the angles on a unit circle.
Recall that the x-coordinate of the coordinates of the terminal point formed by the angle on the unit circle represent the adjacent side of the triangle formed by the terminal side of an angle on a unit circle while the y-coordinate represent the opposite side of the triangle.
#trigonometry #unitcircle
#trigonometry #unitcircle
0:02:32
0:03:35
0:01:56
0:01:20
0:02:03
0:02:41
0:02:22
0:01:59
0:08:42
0:01:46
0:02:12
0:03:31
0:01:42
0:03:38
0:04:37
0:10:59
0:05:38
0:22:47
0:11:43
0:01:00
0:00:57
0:00:35
0:03:53
0:03:56