filmov
tv
Why Geniuses were Confused about Negative Numbers ?

Показать описание
Mathematicians of the past used to struggle a lot with negative numbers. We discuss why in this video.
The idea was adopted from Martin Gardner's book "Penrose tiles to trapdoor ciphers", chapter 11.
(00:00) - minus 1 is weird
(01:16) - Euler is weird
(02:04) - A serious question
(03:25) - We should not ban negative numbers
(05:45) - Negative numbers in real life ?
#numbers
The idea was adopted from Martin Gardner's book "Penrose tiles to trapdoor ciphers", chapter 11.
(00:00) - minus 1 is weird
(01:16) - Euler is weird
(02:04) - A serious question
(03:25) - We should not ban negative numbers
(05:45) - Negative numbers in real life ?
#numbers
Why Geniuses were Confused about Negative Numbers ?
A genius can solve in 10 seconds! 🤯 #shorts #puzzle #riddle
💡 Why You're Not a Genius Yet? 🧠
Math Genius: Unlocking the Power of Numbers and Creativity 📊✨ #lifelessons #motivationalspeech
This artist is genius... #shorts
If you are a genius solve this! Math Game Challenge!!!
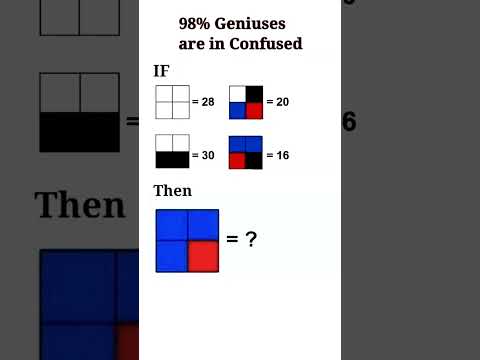
98% geniuses are in confused | High IQ Level #shorts #reasoning
A genius directing trick that confused 'American Psycho' viewers
Napoleon's Daring Plans: The Genius of His Tactics #explorer
Faking Genius at Work is simple, really
What the hell 😱#genius #whatthehell #intelegent
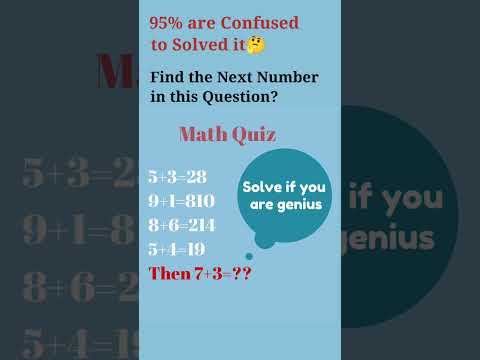
95% geniuses are confused | how many of you can solve this correctly ?? #shorts
If you are genius #intelligent #confused #puzzle #youtube #math #puzzles #hacked
Only for a Genius! Connect 1 to 1, 2 to 2 & 3 to 3 without crossing the lines! #math #youtube
09/10 Geniuses are Confused | can you solve this puzzle #maths #shorts
MOTHERv3 A.I. EVIL GENIUS gets CONFUSED BY MATH MISTAKE
1 or 2? Genius #gachafyp #gachaedit #gachaclub #gachashorts #gacha #gachatrend #gachaclubedit #trend
95% Geniuses are confused | Find the logic, then to solve this puzzle #shorts
91% people confused | only genius can solve this easily #shorts
95% are confused |Solve If you are Genius #mathsquiz #brainteasers
This kid is genius 🧠
99% student are fail 💯💯🔥🔥 only genius can answer it #mamorytest #eyetest #iqtest #braintest...
Riddle |only for Genius😱|IQ test for genius only| IQ test Game|
Riddles You Won't Crack Unless You're a Genius 😱
Комментарии
 0:06:38
0:06:38
 0:00:46
0:00:46
 0:01:00
0:01:00
 0:00:51
0:00:51
 0:00:28
0:00:28
 0:00:28
0:00:28
 0:00:05
0:00:05
 0:00:44
0:00:44
 0:00:46
0:00:46
 0:05:14
0:05:14
 0:00:08
0:00:08
 0:00:06
0:00:06
 0:00:05
0:00:05
 0:00:20
0:00:20
 0:00:05
0:00:05
 0:00:30
0:00:30
 0:00:19
0:00:19
 0:00:06
0:00:06
 0:00:05
0:00:05
 0:00:05
0:00:05
 0:00:08
0:00:08
 0:00:05
0:00:05
 0:00:17
0:00:17
 0:00:38
0:00:38