filmov
tv
Floor and Ceiling Functions in an Exponential Equation

Показать описание
This video is about a floor and a ceiling equation
If you need to post a picture of your solution or idea:
Note: ⌈x⌉=−⌊−x⌋
#ChallengingMathProblems #FloorAndCeilingEquations
EXPLORE:
If you need to post a picture of your solution or idea:
Note: ⌈x⌉=−⌊−x⌋
#ChallengingMathProblems #FloorAndCeilingEquations
EXPLORE:
[Discrete Mathematics] Floor and Ceiling Examples
Floor and Ceiling Functions
Floor and Ceiling Functions #Shorts #math #maths #mathematics #education #learn #learning #study
Greatest Integer Function With Limits & Graphs
Understanding Floor and Ceiling Functions in Mathematics
A ceiling and floor equation
Floor and Ceiling Functions (Discrete Maths)
Floor and Ceil functions with Examples in Urdu/Hindi | Discrete Structures
A Floor and Ceiling Equation, Floor(x-Ceil(x/2))=3
Floor and Ceiling Functions! #shorts
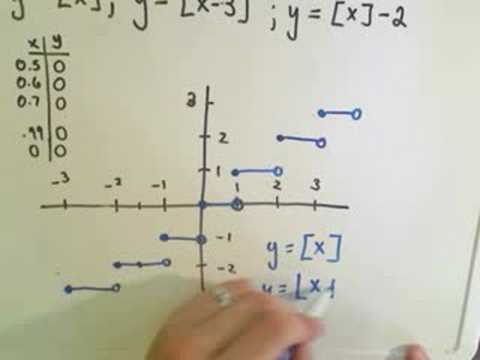
Graphing Floor and Ceiling Functions
Floor and Ceiling Functions, 2nd edition.
Math 2200: Section 4.2 - Floor and Ceiling Functions
Floor and Ceiling values
Floor and Ceiling Functions (Special Functions)
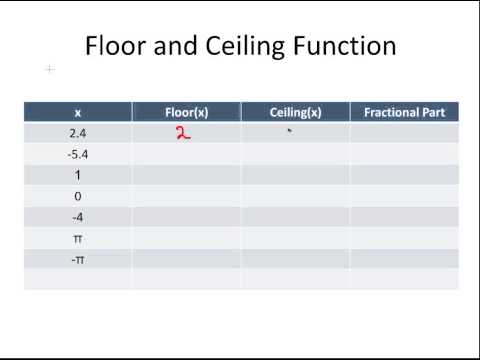
Floor and Ceiling Function Examples
Discrete Math - 2.3.4 Useful Functions to Know
Day 30/100 - CEILING Function in Excel | Excel Function | #youtubeshorts #shorts #excel #function
Floor and Ceiling Function.#math #learnmath #algebra
Graphing the Greatest Integer or Floor Function
Introduction to Floor, Fractional Part, and Ceiling Functions
Floor equation
Floor and Ceiling Functions in an Exponential Equation
FLOOR AND CEILING FUNCTION #numbertheory #youtubeshorts
Комментарии
![[Discrete Mathematics] Floor](https://i.ytimg.com/vi/RxNs4SwP6lk/hqdefault.jpg) 0:05:00
0:05:00
 0:05:09
0:05:09
 0:00:10
0:00:10
 0:16:10
0:16:10
 0:05:05
0:05:05
 0:08:26
0:08:26
 0:06:09
0:06:09
 0:03:01
0:03:01
 0:07:13
0:07:13
 0:00:59
0:00:59
 0:39:13
0:39:13
 0:36:51
0:36:51
 0:17:07
0:17:07
 0:05:18
0:05:18
 0:06:09
0:06:09
 0:06:47
0:06:47
 0:04:51
0:04:51
 0:00:10
0:00:10
 0:00:06
0:00:06
 0:09:06
0:09:06
 0:09:35
0:09:35
 0:12:31
0:12:31
 0:08:36
0:08:36
 0:00:59
0:00:59