L25.2 The method of images - induced charge

#electrodynamics #griffiths #sayphysics
0:00 - Introduction to Induced Surface Charge
0:02 - What is Induced Charge on the Sheet?
0:09 - Finding the Induced Charge on the Sheet
0:15 - Electric Field from a Sheet of Charges
0:22 - Electric Field from an Infinite Sheet of Charges
0:30 - Electric Field Between Two Sheets
0:41 - Electric Field Formula for Two Sheets
0:51 - Relation Between Electric Field and Potential
1:04 - Gradient of Potential and Electric Field
1:17 - Normal Derivative in Electrostatics
1:46 - Explanation of Normal Derivative
2:04 - Surface Normal and Its Direction
2:13 - Normal Derivative Along Z-Axis
2:19 - Mathematical Formulation for Normal Derivative
2:30 - What is the Normal Derivative in Electrostatics?
2:37 - Derivation of Electric Field Formula
2:54 - Using the Gradient of Potential
3:01 - Calculating Charge from the Gradient
3:09 - Using Gradient to Find Induced Charge
3:18 - Formula for Charge in Terms of Potential
3:40 - Electric Field and Charge at z = 0
3:55 - Potential Difference and Induced Charge
4:06 - Derivation of Charge Formula
4:39 - Derivative of Potential with Respect to Z
4:55 - Simplifying Charge Formula
5:05 - Detailed Calculation Steps
5:18 - Deriving the Formula for Charge Distribution
5:36 - Simplification of Charge Distribution Formula
6:03 - Derivative and Simplification Process
6:30 - Simplified Charge Distribution Formula
7:01 - Calculating Charge and Potential
7:19 - Final Formula for Induced Charge
7:33 - Putting z = 0 in Charge Formula
8:01 - Final Simplified Expression for Charge
8:28 - Calculation of Charge Distribution
8:46 - Resulting Expression for Charge
9:06 - Expression for Charge with z = 0
9:32 - Final Charge Formula
10:01 - Deriving Total Charge on the Sheet
10:28 - Surface Integral to Find Total Charge
10:53 - Final Formula for Total Induced Charge
11:15 - Final Expression for Induced Surface Charge
12:02 - Surface Integration for Total Charge
12:25 - Total Charge Calculation
12:46 - Formula for Surface Integral
13:06 - Conclusion and Total Charge Integration

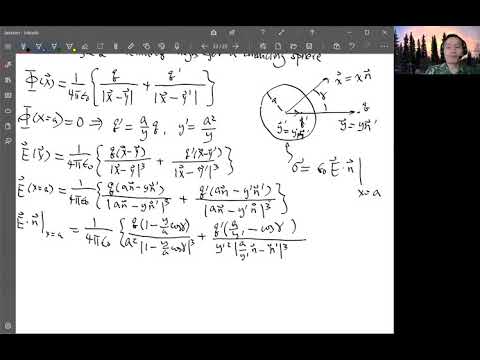
The method of images in electrodynamics involves a clever mathematical technique to simplify complex boundary value problems. This method leverages the principle of mirror charges to create a virtual image system that mimics the behavior of the actual charge distribution. By strategically placing these imaginary charges, one can construct a scenario with known boundary conditions, facilitating the solution of electrostatic and magnetostatic problems. DJ Griffiths' elucidation of the method of images provides.
"method of images," "electrodynamics," "DJ Griffiths," "mirror charges," "boundary value problems," "electromagnetic theory," "virtual image system," "charge distribution," "electrostatic problems," "magnetostatic problems."

[vishnuvpriya]

Your teaching style is incredible! The way you explain complex concepts is crystal clear and easy to understand. It really helps me grasp the concept with confidence. Thank you for making learning so enjoyable and accessible. Keep up the fantastic work!"sir

[sabasabir]

Your teaching style is verstile. Appreciation from saudia arabia we all fellows follows your lecture .Thank you so much

[AhmedKhaleelAhmedAhmed]

thank you so much
can you update electromagnetic please your teaching so good thank you again