filmov
tv
Integrate Sin(3x)Cos(4x) - No Trig Identities Needed! Going in a Loop!

Показать описание
In this video, we use the traditional method of integration by parts to find the antiderivative of a product of two different trigonometric function: sin(3x)cos(4x).
It is presented in textbooks that we are using the product-to-sum formula to turn this expression into a sum. But actually, we don't need to.
It does not matter whether we use u = sin(3x) or u = cos(4x), we are still going to get back to the original problem. So it looks like we are going in a loop!
See another video in which we go in a loop when integrating e^(-2x)sin(3x):
See how to integrate this without using integration by parts:
Please help me by subscribing to my YouTube channel. I want to use my free time to make a lot of math videos to help others and to make education available to the world. Your Likes and Subscribing will help this channel be reached by more people. Thank you!
Follow me:
It is presented in textbooks that we are using the product-to-sum formula to turn this expression into a sum. But actually, we don't need to.
It does not matter whether we use u = sin(3x) or u = cos(4x), we are still going to get back to the original problem. So it looks like we are going in a loop!
See another video in which we go in a loop when integrating e^(-2x)sin(3x):
See how to integrate this without using integration by parts:
Please help me by subscribing to my YouTube channel. I want to use my free time to make a lot of math videos to help others and to make education available to the world. Your Likes and Subscribing will help this channel be reached by more people. Thank you!
Follow me:
Integrate Sin(3x)Cos(4x) - No Trig Identities Needed! Going in a Loop!
Integrate Sin(3x)Cos(4x) by Tabular Method - No Trig Identities Needed | Glass of Numbers
How to Integrate ∫sin^3(x)cos^4(x)dx
∫ sin 3x cos 4x dx INTEGRATION PROBLEM 30
Integral of sin^3(x)cos^4(x) (substitution)
when calculus students use trig identities too early
Trigonometric Integrals
Find the integrals of the function ∫ sin 3x cos 4x dx
TRIG INTEGRATION sin3xcos3x
How REAL Men Integrate Functions
Trigonometric Integrals Powers of Sine and Cosine cos^4(3x)
sin3x + sinx = cos6x + cos4x | 12 | GENERAL SOLUTIONS OF TRIGNOMETRIC EQUATIONS | MATHS | CHHAY...
cos(3x)cos(4x) express the product as a sum
12Th Ex 7.3 Q 2 Integrate sin 3x cos 4x dx
Evaluate integration of sin^3x cos^4x dx
Integration of sum and product of Trig Strategy cos4x cos7x Trigonometric Substitution
Integral of sin(3x)*cos(x)
Trigonometry Formulas -2
How to Integrate Sin 4x and Cos 3x type Integrals. Integral of Sin4x. Integral of Cos3x. Integration
Integral Fungsi Trigonometri 4 sin 3x cos x dx
Trying transition video for the first time 💙😂 || #transformation #transition #shorts #viralvideo...
JEE Aspirants ka Sach 💔 #JEE #JEEMain #Shorts
Integral sin3x cos4x dx
∫sin^3(x)/(cos^4(x)+cos^6(x)) dx [-1, 1]. Solving Challenging integration but simple solution!
Комментарии
 0:11:56
0:11:56
 0:09:41
0:09:41
 0:06:12
0:06:12
 0:03:30
0:03:30
 0:02:38
0:02:38
 0:00:43
0:00:43
 0:31:29
0:31:29
 0:02:55
0:02:55
 0:00:57
0:00:57
 0:00:35
0:00:35
 0:05:48
0:05:48
 0:07:47
0:07:47
 0:01:18
0:01:18
 0:07:08
0:07:08
 0:01:40
0:01:40
 0:03:23
0:03:23
 0:04:51
0:04:51
 0:00:05
0:00:05
 0:01:14
0:01:14
 0:03:13
0:03:13
 0:00:15
0:00:15
 0:00:12
0:00:12
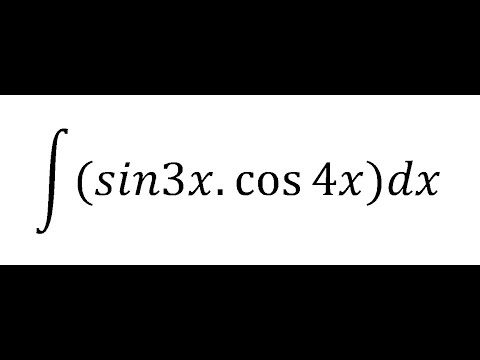 0:01:53
0:01:53
 0:01:01
0:01:01