❖ The Definite Integral - Understanding the Definition ❖

The Definite Integral: Understanding the Definition
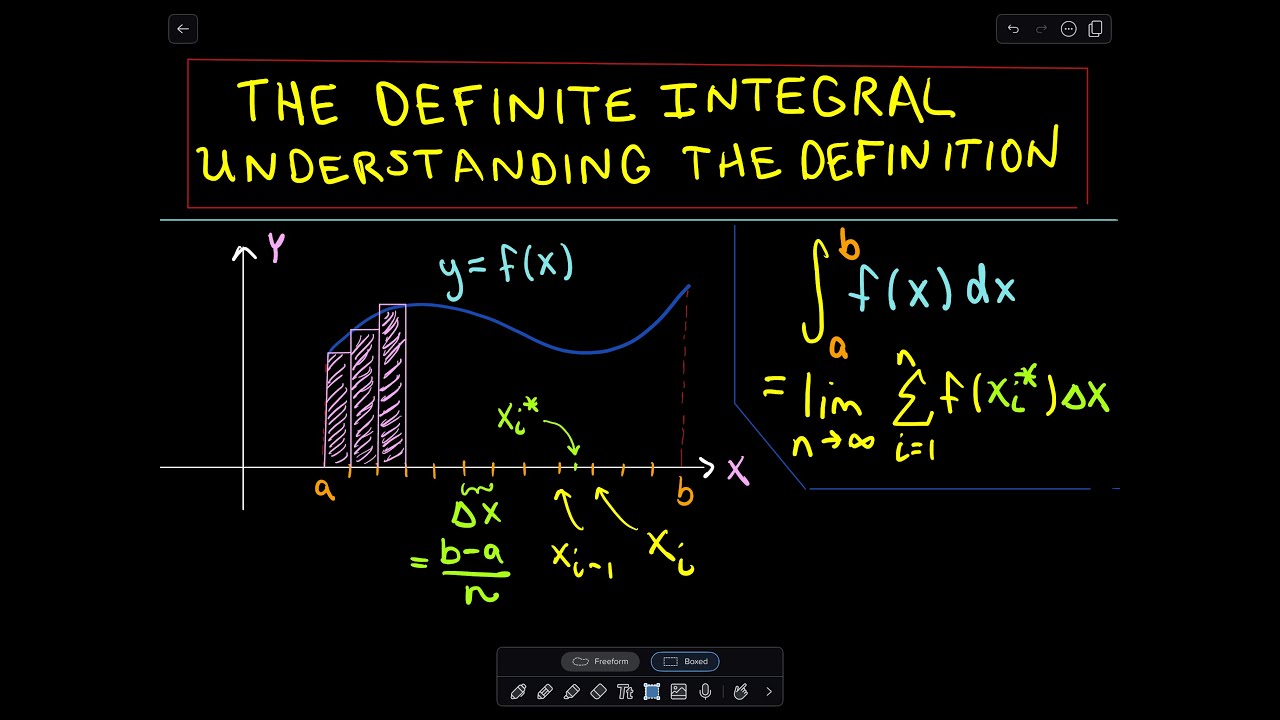
In this video, we dive deep into the definition of the definite integral, exploring its conceptual meaning and breaking down the limit process involved in defining the integral. By understanding how the sum of the areas of rectangles approaches the area under a curve as the number of rectangles increases, we build the foundation for understanding what a definite integral represents. Note that this video focuses on the theory and definition, rather than the computation of definite integrals.

What You Will Learn:
The definition of the definite integral and its connection to the area under a curve.
How to interpret the limit of Riemann sums as a way to understand the integral.
The process of dividing an interval into subintervals and evaluating the function at sample points.
A conceptual understanding of how the integral is built from sums of areas.
📚 Check out my book: 1001 Calculus Problems for Dummies for more practice!

👍 **If you find this video helpful, please like, share, and subscribe for more math tutorials!

Support My Work:

#Calculus #DefiniteIntegral #MathTutorial #PatrickJMT #RiemannSums #IntegralDefinition #Mathematics #LimitProcess #IntegralCalculus #MathHelp #ConceptualUnderstanding #Precalculus #Education #Functions #Integrals

[TamNguyenMinh-opiq]

It's 2023 now and your videos have helped me with Calculus in College. Thank you so much.

[AndrewSmithDev]

Why am I paying 1000 dollars to attend a class where my professor is completely worthless at explaining these ideas when I can come on youtube and get a better explanation for free

[birdflocked]

You are a lifesaver when Calculus starts to get confusing.

[cherriewong]

Thank you Patrick! Never did i feel bored when watching your enthusiastic calculus teaching! Because of your clear and detailed explanations, I eventually excelled in my final !!!!YOU ARE AWESOME!!!

[MrMoeqt]

You're amazing! You and Khan academy helped me start my calculus. Right now I'm 13, and I started learning basic derivatives at late 12, at first it was so hard, it just looked like d's and x's etc... But I stuck at it and then I finally understood the power rule for taking derivatives, I FELT LIKE A GENIUS:D. From then on I kept going and eventually my knowledge of derivatives came to the point where I can find any derivatives easily, now I'm moving on to integrals because of you! Thanks loads!

[gaoalexander]

My professor explained this to me in class today. I must say that I was clueless. Maybe its the fact that he assumes its easy since he already understands it, but not you. You assume that we are clueless, which is a good thing. You just made my day a lot better! 

[patrickjmt]

that, my friend, is truly the magical part

[Renee]

Thank you so much! I'm at the point of calculus where things began to become a whole other language to me and my mind is still trying to process things even at night ruining my sleep. This video helped clear the fog in my mind.

[QWEEKEN]

Cal final in 4 hours. Your a life saver!

[patrickjmt]

it represents any point from the 'i-th' interval (it does not have to be a left endpoint or right endpoint, etc)

[macmos]

These videos are just awesome to watch after reading my calculus book until you fully understand it. It reinforces what I've learned.

[IbombYourAss]

I can't tell you how much I appreciate your videos - my Calculus class is in the morning, and when I try to do practice problems after class, I can't remember anything I 'learned.'

Not only do your videos help me relearn it, it helps me remember what we actually did in class, so I strengthen my understanding even more.

[IDidactI]

When you differentiate, you divide a tiny slice of y by a tiny slice of x i.e. dy/dx. That ratio gives you a slope, which hopefully you understand. So, dy/dx = f'(x). Okay so what happens if we multiply both sides of that by dx, we get dy = f'(x) * dx. So to find y, add up all the 'dy's. That's what the integral does. Also, look at the equation. f'(x) is the height of the function and dx is the width. Area of a rectangle = height * width, right? You can figure out the rest ;)

[scorpion]

Thank God for youtube!!! Your video filled in all the holes or questions i had from class lecture beautifully....Words can't capture the relief of finally "getting it". Thx

[Salamero]

seriously you should be getting some kind of nobel prize for teaching excellence, your public service should be recognized some day by all of your students you never met, thank you kindly.

[ProBro]

you'r better than any prof i've ever had for math

[amandaoliver]

I love your vids but the sound quality on this one makes it unbearable to watch.

[magicguy]

Approximation is the foundation of all of single-variable calculus. When trying to understand tangents, we started with an approximation and arrived at the derivative thru use of limits

[Hulahoopish]

I just got my degree in mechanical engineering, and I want you to know, that legitimately might not have happened without you. I cannot thank you enough for these tutorials.

[CReePiNxMeaDoWs]

Explained it crystal clear and I just now understand it the night before my Calc I final. You sir, are a life saver and I applaud your work.