Pi is IRRATIONAL: animation of a gorgeous proof

NEW (Christmas 2019). Two ways to support Mathologer
(see the Patreon page for details)

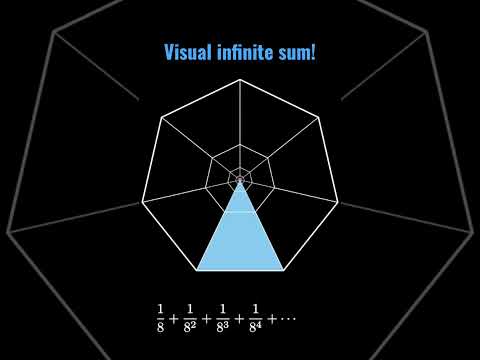
This video is my best shot at animating and explaining my favourite proof that pi is irrational. It is due to the Swiss mathematician Johann Lambert who published it over 250 years ago.

Anyway it's been an absolute killer to put this video together and overall this is probably the most ambitious topic I've tackled so far. I really hope that a lot of you will get something out of it. If you do please let me know :) Also, as usual, please consider contributing subtitles in your native language (English and Russian are under control, but everything else goes).

Have a close look and you'll see that as n goes to infinity all the highlighted terms approach 1. What's left are the Maclaurin series for sin x on top and that for cos x at the bottom and this then goes a long way towards showing that those partial fractions really tend to tan x.

Today's main t-shirt I got from from Zazzle:
(there are lots of places that sell "HO cubed" t-shirts)


Special thanks to my friend Marty Ross for lots of feedback on the slideshow and some good-humoured heckling while we were recording the video. Thank you also to Danil Dimitriev for his ongoing Russian support of this channel.

Merry Christmas!

[bluebrown]

Fantastic! One of the most accessible proofs of this fact I’ve ever seen.

[Mathologer]

This video is my best shot at animating and explaining my favourite proof that pi is irrational. It is due to the Swiss mathematician Johann Lambert who published it over 250 years ago.


Anyway it's been an absolute killer to put this video together and overall this is probably the most ambitious topic I've tackled so far. I really hope that a lot of you will get something out of it. If you do please let me know :) Also, as usual, please consider contributing subtitles in your native language (English and Russian are under control, but everything else goes).

Today's main t-shirt I got from from Zazzle:
(there are lots of places that sell "HO cubed" t-shirts)

Merry Christmas,

burkard

[aakash_kul]

That shirt! 25 base 10 = 31 base 8. In other words, 25 Dec = 31 Oct. Merry Halloween!

[wrpbeater]

"Welcome to the last Mathologer video"
- WHAT
"... of the year"
- phew

[enough_b]

Regarding the first puzzle :

log10(2) cannot be rational. The same method can be used, and it is trivial to show that no power of two can be divisible by a power of 10 (Except 10^0, of course).

log7(8/9) cannot be rational either. log7(8/9) = log7(8) - log7(9); and log7(8) cannot be rational since 7 is odd and 8 is even.

This leaves the woodlog. We need to go down two paths for this, assuming the drawing represents a real situation :

1. Either woodlogs are incapable of reason or speech. In which case, this one could be part of the few rational/speaking ones, but it is unlikely such a behavior would evolve so fast without intermediary steps.

2. Or woodlogs are capable of reason and speech, usually. Yet, they never speak. They get chopped, sawed, burnt, and they still don’t speak. If they are both rational and willing to go through this shutting up, they must have a damn good reason. Yet this log just broke millenias of omerta over a pun. I can’t imagine a situation in which that’s rational.

[unvergebeneid]

To answer the puzzle: none of those logs is rational. Not even the one claiming it is. I mean, come on, a piece of wood shouting out statements on its own rationality? That's completely bonkers!

[thecubeur]

7:26 Small mistake, the second term of the expansion of cos(x) should be of degree 2.

[flymypg]

SPLENDID! More please! You and 3B1B are both doing such great work with math-related animations.

[lukecow]

This proof is far more natural than any proof of this I've ever seen. Please make the video you mentioned at 15:56 :)

[vvmcmurdo]

Can I just say that Mathologer is one of the most cranckiest, craziest, wackiest, nerdiest and most likable personalities in YouTube? Hello?
Love these amazing videos!

[nujuat]

Wow that last part of the proof was really nice :)

[Tiqerboy]

I can only imagine how awesome Lambert must have felt that night when he finished that proof!

[semicharmedkindofguy]

Seeing you so cheerful about math on all your videos makes me happy. The joy you exude is infectious! Happy holidays!

[IllusionzZBxD]

Not only is this video itself a great example of making a proof accessible, you are a great example of an educator that genuinely enjoys teaching others. You certainly make me feel more confident that I want to teach maths myself to others.

[vighnesh]

I have seen this video over 10 times and I still get the chills when it gets proved that PI is irrational. Wonderful work. I know you worked very hard to make this animation and I must tell you, your hard work has been fruitful to many math lovers out there. I hope you never stop making such videos. Love from India.

[michalbotor]

i like how you present proofs sir. showing their sketch first and then filling in the gaps makes it both easy to understand them and remember, and leaves no room to get lost while we fill in the gaps later on. i recall countless times being totally lost after already like a half hour long proof done in a from a to z fashion what are we even proving in the first place..

[jonathanwalther]

I'm not a mathematician, and I love this channel. Thanks for all the sophisticated work.

[phoquenahol]

At 5:52, let 2+1/(1+1/(2+1/(1+...)=x. Then 2+1/(1+(1/x))=x.
Simplifying results in the quadratic x^2-2x-2 which has the positive root 1+sqrt(3).
The desired value is x-1=sqrt(3).
At 17:30, let 2/3-(2/3-(2/3-...)=x. Then 2/(3-x)=x which results in the quadratic x^2-3x+2 which has roots 1 and 2.
In general, consider the infinite fraction which becomes the quadratic x^2-(k+1)x+k which has roots 1 and k. Note this holds for all real k.
Side note: I don't know how to prove why the fraction must equal 1 instead of k. If somebody can prove this, that would be great.

[Richard_Stroker]

log_10(2) = a/b [for some integers a, b, with b not zero]
2 = 10^(a/b)
2^b = 10^a
2^b = (5^a)(2^a)
5 divides 2
Contradiction. Therefore we conclude that log_10(2) is irrational.

log_7(8/9) = a/b
8/9 = 7^(a/b)
(8^b)/(9^b) = 7^a
8^b = (7^a)(9^b) = 2^3b
7 divides 2
Contradiction. Therefore we conclude that log_7(8/9) is irrational.

[BryceRosenwald]

I love how much fun these guys always have filming their videos. It always makes me happy.