filmov
tv
Mastering Functional Equations in Math Olympiads
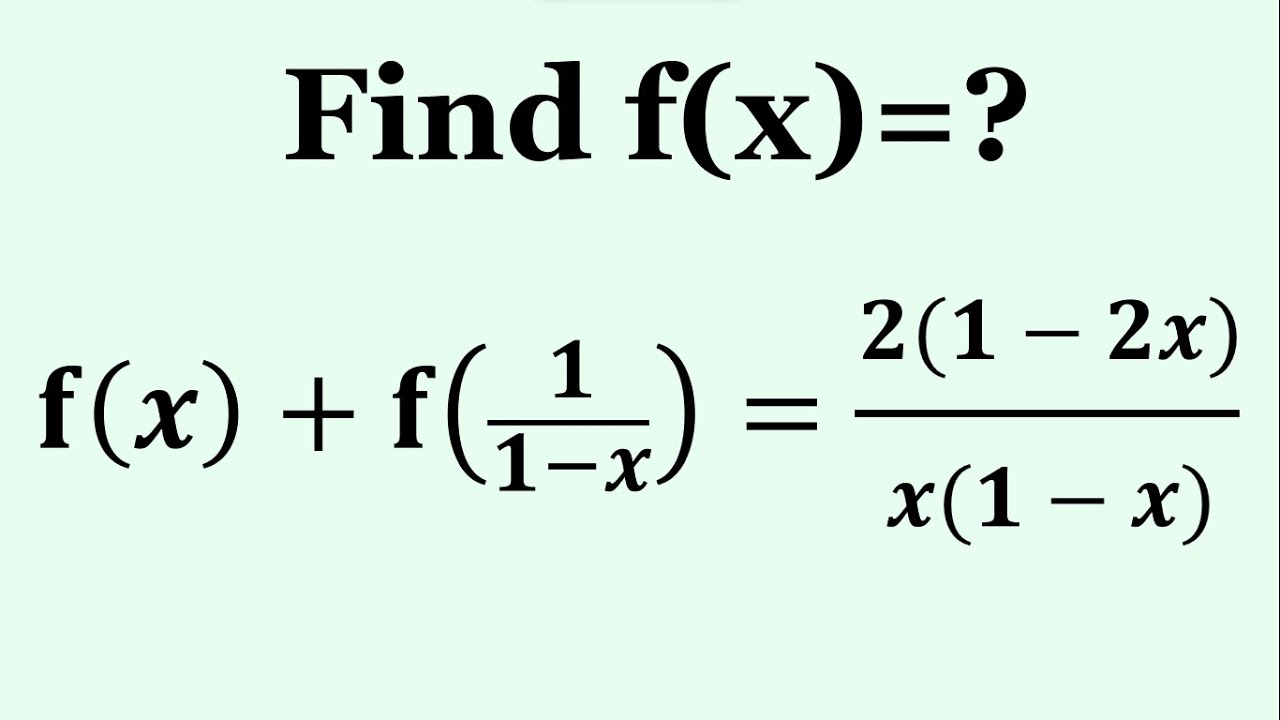
Показать описание
Mastering Functional Equations in Math Olympiads
🏆 Dive deep into the realm of Math Olympiads and conquer functional equations like a true champion! 💡 Join us as we unveil expert strategies, solve intricate problems, and empower you to excel in the realm of competition math. 🧠 From understanding the fundamentals to mastering advanced techniques, this guide is your roadmap to success in navigating functional equations in Olympiad contests. 🌟 Equip yourself with the skills and knowledge needed to tackle any challenge that comes your way! #MathOlympiad #FunctionalEquations #CompetitionMath #ProblemSolving #Mathematics #OlympiadPreparation #Mathletes #Logic #CriticalThinking #Education #MathIsFun #Puzzle #MathematicsEducation
📘 Topics Covered:
Understanding the basics of functional equations
Step-by-step solutions for common types: substitutions
Advanced techniques of algebraic manipulations and change of variable
Solving system of functional equations
Practical calculation of function f(x)
Timestamps:
0:00 Introduction
1:30 Simplifying expressions
3:06 Replacement of variable
5:40 Solving functional equation
8:40 Finding f(x)
Don't forget to like, subscribe, and comment with your thoughts and solutions! Let the mathematical journey begin! 🎓🔢✨
Thanks for Watching!!
@infyGyan
🏆 Dive deep into the realm of Math Olympiads and conquer functional equations like a true champion! 💡 Join us as we unveil expert strategies, solve intricate problems, and empower you to excel in the realm of competition math. 🧠 From understanding the fundamentals to mastering advanced techniques, this guide is your roadmap to success in navigating functional equations in Olympiad contests. 🌟 Equip yourself with the skills and knowledge needed to tackle any challenge that comes your way! #MathOlympiad #FunctionalEquations #CompetitionMath #ProblemSolving #Mathematics #OlympiadPreparation #Mathletes #Logic #CriticalThinking #Education #MathIsFun #Puzzle #MathematicsEducation
📘 Topics Covered:
Understanding the basics of functional equations
Step-by-step solutions for common types: substitutions
Advanced techniques of algebraic manipulations and change of variable
Solving system of functional equations
Practical calculation of function f(x)
Timestamps:
0:00 Introduction
1:30 Simplifying expressions
3:06 Replacement of variable
5:40 Solving functional equation
8:40 Finding f(x)
Don't forget to like, subscribe, and comment with your thoughts and solutions! Let the mathematical journey begin! 🎓🔢✨
Thanks for Watching!!
@infyGyan
Комментарии
 0:09:03
0:09:03
 0:10:11
0:10:11
 0:08:38
0:08:38
 0:11:48
0:11:48
 0:08:42
0:08:42
 0:09:43
0:09:43
 0:00:58
0:00:58
 0:09:01
0:09:01
 0:15:30
0:15:30
 0:02:57
0:02:57
 0:18:45
0:18:45
 0:00:48
0:00:48
 0:00:52
0:00:52
 0:32:05
0:32:05
 0:00:52
0:00:52
 0:05:58
0:05:58
 0:00:54
0:00:54
 0:00:29
0:00:29
 0:00:58
0:00:58
 0:00:59
0:00:59
 0:00:40
0:00:40
 0:00:59
0:00:59
 0:11:03
0:11:03
 0:00:09
0:00:09