filmov
tv
0.999... = 1 [PROOF]

Показать описание
This is my proof that I devised to show that 0.999... [nonterminating] is in fact equal to 1.
It will work for 2.999... = 3, 1.999... = 2
It will NOT work on anything that is between 9 and 0 (0.111..., 0.777...)
Up Next:
Why Infinity Renders to Zero!
It will work for 2.999... = 3, 1.999... = 2
It will NOT work on anything that is between 9 and 0 (0.111..., 0.777...)
Up Next:
Why Infinity Renders to Zero!
Does 0.999... = 1?
0.999999… = 1
Every PROOF you've seen that .999... = 1 is WRONG
I'm Settling This Math Debate Forever (.99 repeating = 1)
Simplest proof that 0 999 is not equal to 1
0 999... Is 1 Here’s Proof!
Mathematical Proof that 0 999...= 1
How to prove that 0•999•••=1 just by observation #shorts |@goymath
Can You Prove That 0 999 is Actually Equal to 1
Why 0 999 1 The Math Proof That Will Break Your Brain
0 9999...= 1 Proof
0.999... Repeating Is Equal To 1, But Something Like It Is Not (Introduction To The Surreal Numbers)
Beyond Infinity Number Comparison
Why 0 999 = 1 Mind blowing proof (with fractions)
The Simpleton's Proof that 1 Does Not Equal 0 99999
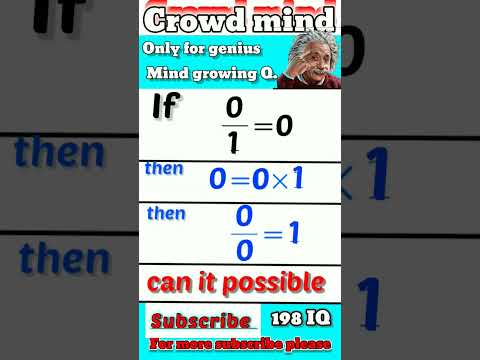
0÷0=1 proof 😱 || can it possible #shorts #viral #mathquiz
This Video is 0 Seconds Long
O.999 Repeating = 1 | Algebraic Proof | You should know this!
Chat GPT says, there's NO PROOF for 0 999 =1!!
Why 1% Battery Last So Long ☹️
The 360-Page Proof That 1+1=2
What the 5th Dimension Looks Like
Multiples of 8 😎 #Shorts #math #maths #mathematics
🔴∞ × 0 = 1 , prove that #infinity #math #viral #ytvideo
Комментарии
 0:02:27
0:02:27
 0:01:00
0:01:00
 0:09:25
0:09:25
 0:04:11
0:04:11
 0:01:59
0:01:59
 0:00:54
0:00:54
 0:02:43
0:02:43
 0:00:23
0:00:23
 0:01:45
0:01:45
 0:02:17
0:02:17
 0:00:52
0:00:52
 0:08:08
0:08:08
 0:07:00
0:07:00
 0:00:51
0:00:51
 0:00:46
0:00:46
 0:00:06
0:00:06
 0:00:22
0:00:22
 0:01:22
0:01:22
 0:06:03
0:06:03
 0:00:25
0:00:25
 0:06:03
0:06:03
 0:00:59
0:00:59
 0:00:20
0:00:20
 0:00:26
0:00:26