filmov
tv
Pillai Grad Lecture 10A 'Power Spectrum of Stationary Stochastic Processes' (1/2)

Показать описание
Classic Wiener-Khinchine theorem, where the power spectrum of a stationary stochastic process is shown to be the ordinary Fourier transform of its autocorrelation function. Derivation of the power spectrum of a stationary stochastic process as the Fourier transform of its autocorrelation function.
Pillai Grad Lecture 10A 'Power Spectrum of Stationary Stochastic Processes' (1/2)
Pillai: Grad Lecture 10B 'Power Spectrum of Stationary Stochastic Processes' (2/2)
Pillai 'Power Spectrum of a Damped Sinc Function'
Pillai 'Whitening Filter'
PIllai 'Fourier Transforms'
Pillai 'Autocorrelation Function'
Pillai: Power Spectrum of Stationary Stochastic Processes
Pillai EL6333 Lecture 9 April 10, 2014 'Introduction to Stochastic Processes'
Pillai: ARMA Processes
Pillai Grad Lecture 8 'Basics of Stationary Stochastic Processes'
Pillai 'Variance and Covariance'
Pillai: Autocorrelations and Non-negative Definite Matrices
Power Spectral Density of a Signal Exercise
Pillai: Spectrum Extension Problem
Pillai: Grad Probability Lect. 1a: Conditional Probability and Independence
Power Spectrum
Pillai: Grad Probability: Bayes' Theorem and Inference
Pillai: M-ary Hypothesis Testing
Pillai 'Randomly Sampled Stochastic Processes Y(n) = X( ∑ ζ_i ) '
Pillai 'Matched Filter' (Version -2)
Pillai 'Stochastic Process applied to an LTI System'
Linear System Output Random Process Power
Pillai: Random Processes to Linear Systems
SPECTRAL DENSITY PROBLEM 4
Комментарии
 0:37:05
0:37:05
 0:25:31
0:25:31
 0:27:09
0:27:09
 0:34:29
0:34:29
 0:33:02
0:33:02
 0:09:21
0:09:21
 0:31:23
0:31:23
 2:43:12
2:43:12
 0:46:21
0:46:21
 0:34:48
0:34:48
 0:32:19
0:32:19
 0:15:21
0:15:21
 0:01:01
0:01:01
 0:45:27
0:45:27
 0:09:27
0:09:27
 0:28:57
0:28:57
 0:17:57
0:17:57
 0:15:41
0:15:41
 0:13:40
0:13:40
 0:39:08
0:39:08
 0:09:07
0:09:07
 0:04:15
0:04:15
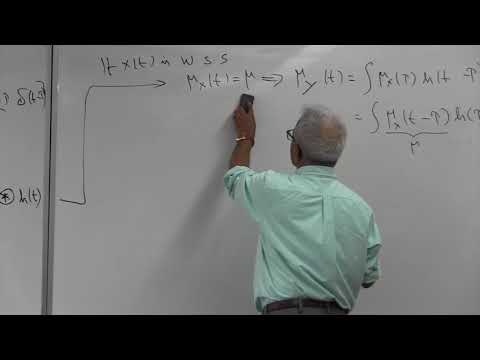 0:29:49
0:29:49
 0:04:48
0:04:48