filmov
tv
Pillai: Random Processes to Linear Systems
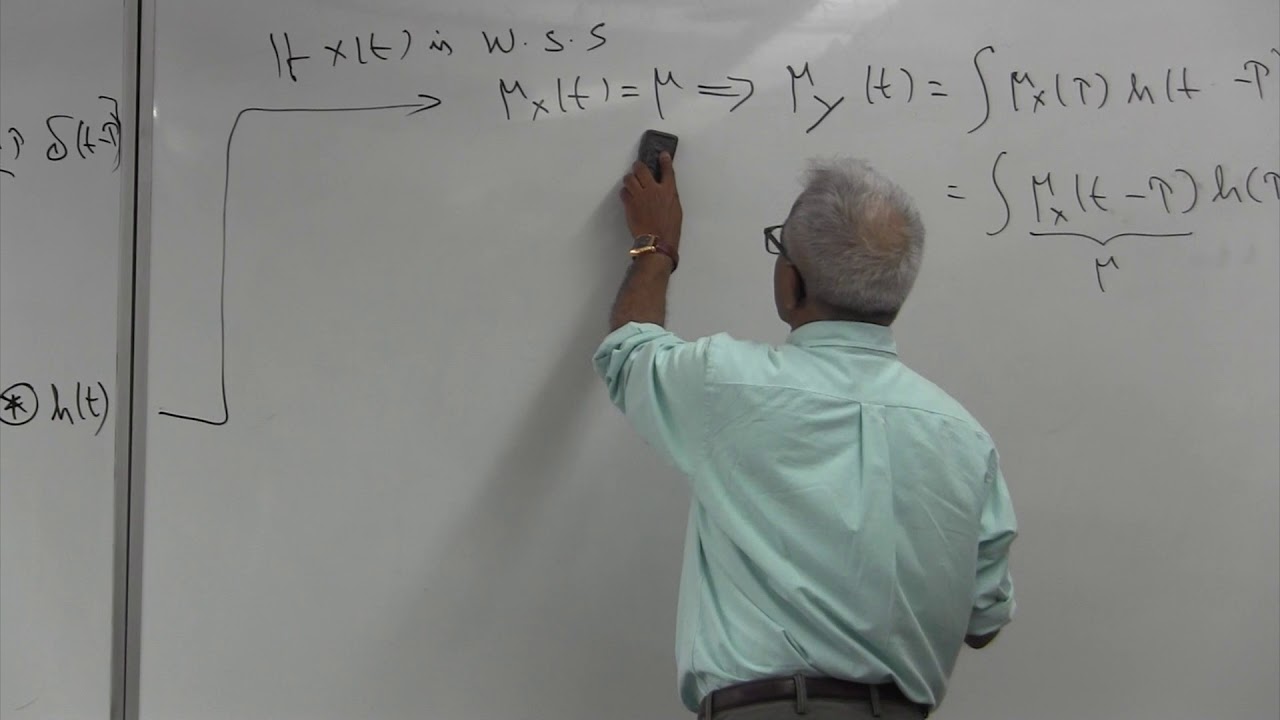
Показать описание
Input-Output characterization of random processes to linear time-invariant Systems (LTI) is considered here. Mean and auto-correlation function of output process is expressed in terms of those of the input process and the system impulse response.
0:29:49
Pillai: Random Processes to Linear Systems
0:50:11
Pillai Grad Lecture 9 'Stochastic Inputs to Linear Systems'
0:05:22
Pillai: Linear Transformation of Jointly Gaussian Random Variables
0:12:26
Pillai 'Mean and Variance of Linear combinations of Two Random Variables'
0:33:33
Pillai: One Function of Two Random Variables Z = X + Y (Part 1 of 6)
0:09:07
Pillai 'Stochastic Process applied to an LTI System'
0:17:18
Pillai: Gaussian Processes
0:27:24
Pillai 'Linear Combinations of Jointly Gaussian Random Variables'
0:13:18
Pillai 'Randomly Compressed Stochastic Processes'
0:07:01
GAUSSIAN RANDOM PROCESSES # POISSON RANDOM PROCESSES
0:10:05
Pillai 'Stationary Complex Gaussian Processes' (Part 1 of 5)
0:04:53
Pillai Probability 'The Best Linear Estimator' (1/2)
0:13:56
Gaussian Random Process Input/Output Relationship
0:04:15
Linear System Output Random Process Power
0:13:28
Pillai 'Stationary Complex Gaussian Processes' (Part 3 of 5)
0:09:46
LINEAR SYSTEM RANDOM INPUTS INTRDOUCTION AND RESULT
0:11:57
Linear Systems with Stochastic Inputs
0:15:46
Pillai: Grad lecture 11 'Discrete Time Stochastic Processes'
0:23:29
Pillai: Linear Prediction Method
0:05:29
3. Transformations of Random Variables: Linear Transformations
0:08:56
Pillai Probability 'Non-stationary to Stationary Behavior Using Non-linearity'
0:19:16
Pillai: Capon vs Linear Prediction Processing
1:17:41
5. Stochastic Processes I
0:18:37
Pillai: One Function of Two Random Variables Z = sqrt [X^2 + Y^2] (Part 3 of 6)
Комментарии