filmov
tv
Law of Sine Ambiguous Case

Показать описание
I introduce the Ambiguous Case for Law of Sine.
1 Triangle 2:12 and 23:00
0 Triangle 7:36
2 Triangles 11:25
Summary of Steps at 28:46
Law of Sine Introduction
Law of Cosine Introduction
Applications of Law of Sine and Law of Cosine
1 Triangle 2:12 and 23:00
0 Triangle 7:36
2 Triangles 11:25
Summary of Steps at 28:46
Law of Sine Introduction
Law of Cosine Introduction
Applications of Law of Sine and Law of Cosine
The Ambiguous Case for Sine Law - Nerdstudy
Ambiguous Case Law of Sines
Ambiguous case law of sines two triangles SSA
Law of Sines (SSA) Ambiguous Case 2 Triangles Possible
Ambiguous Case of the Law of Sines (SSA)
Law of Sines AAS, ASA, SSA Ambiguous Case
The Law of Sines: The Ambiguous Case
Ambiguous Cases, Law of Sines
Law of Sines, Basic Introduction, AAS & SSA - One Solution, Two Solutions vs No Solution, Trigon...
Sine Rule: The Ambiguous Case
LAW OF SINES AND THE AMBIGUOUS CASE || GRADE 9 MATHEMATICS Q4
Law of Sines Ambiguous Case Two Triangles
law of sines, the ambiguous case
Law of sines Ambiguous case two solutions
Law of Sine Ambiguous Case
Math 20-1: Ambiguous Case of the Sine Law
MCR3U1: 5.6 The Sine Law Ambiguous Case (Part 1 of 2)
Ambiguous Case of the Sine Law • [2.3c] Pre-Calculus 11
Ambiguous Case-Law of sine
Unit 2 3 4 Ambiguous Case of Sine Law Part 1
ambiguous case os the sine law introduction
Ambiguous case of the law of sine ( Problems) - Pre Calculus
Functions 5.6 The Sine Law and the AMBIGUOUS Case!
How to determine if you have 0,1 or 2 triangles for the ambiguous case
Комментарии
 0:07:23
0:07:23
 0:05:46
0:05:46
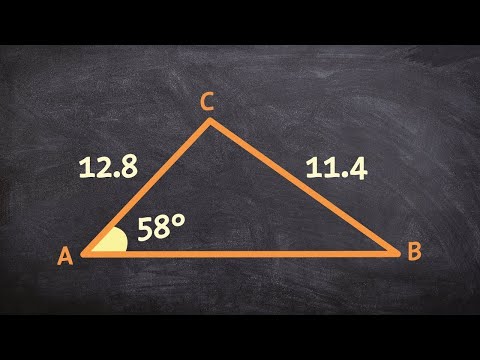 0:15:58
0:15:58
 0:08:23
0:08:23
 0:17:39
0:17:39
 0:17:08
0:17:08
 0:10:04
0:10:04
 0:09:29
0:09:29
 0:21:12
0:21:12
 0:11:25
0:11:25
 0:43:49
0:43:49
 0:10:32
0:10:32
 0:08:49
0:08:49
 0:15:02
0:15:02
 0:31:45
0:31:45
 0:11:54
0:11:54
 0:07:16
0:07:16
 0:17:10
0:17:10
 0:51:24
0:51:24
 0:06:57
0:06:57
 0:08:07
0:08:07
 0:22:24
0:22:24
 0:15:47
0:15:47
 0:03:05
0:03:05