filmov
tv
Maclaurin series of sin(x) | Series | AP Calculus BC | Khan Academy
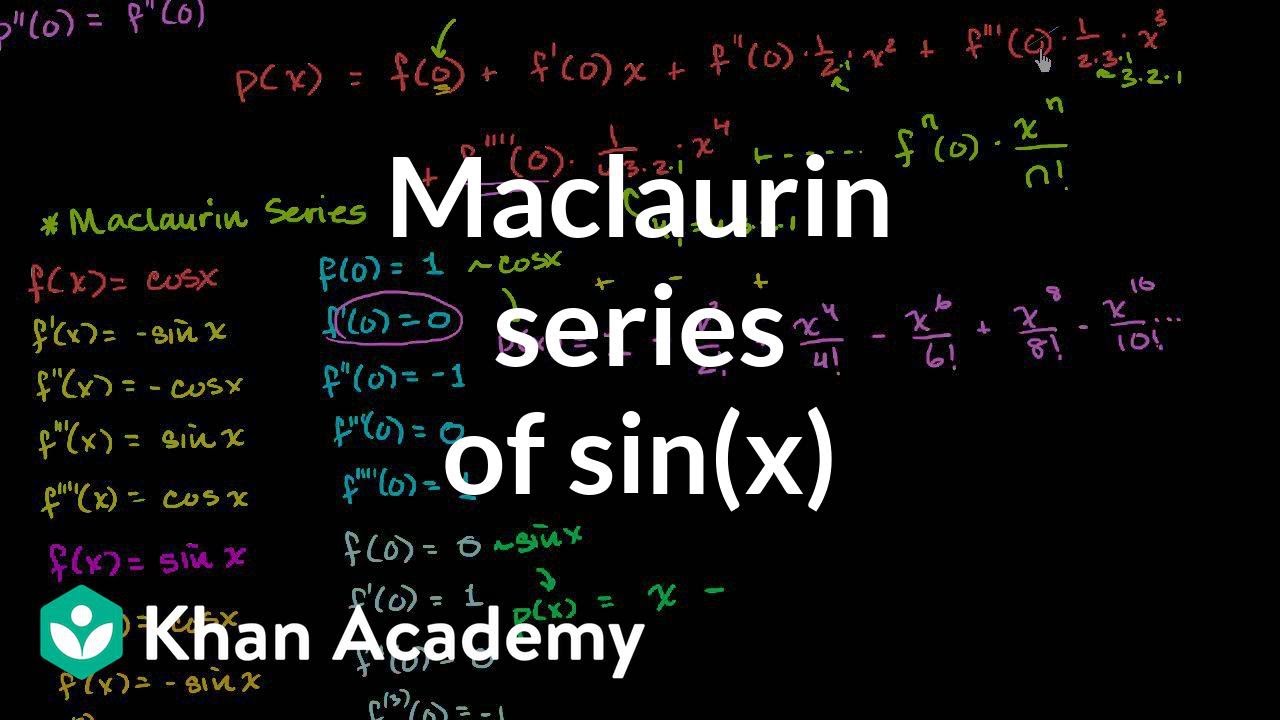
Показать описание
Approximating sin(x) with a Maclaurin series (which is like a Taylor polynomial centered at x=0 with infinitely many terms). It turns out that this series is exactly the same as the function itself! Created by Sal Khan.
AP Calculus BC on Khan Academy: Learn AP Calculus BC - everything from AP Calculus AB plus a few extra goodies, such as Taylor series, to prepare you for the AP Test
For free. For everyone. Forever. #YouCanLearnAnything
❖ Taylor / Maclaurin Series for Sin (x) ❖
Maclaurin series of sin(x) | Series | AP Calculus BC | Khan Academy
Maclaurin Series for sin x (Calculus 2)
Maclaurin series of sin x
A-Level Further Maths D6-04 Maclaurin Series: sin(x)
Taylor series for sin(x) and cos(x), Single Variable Calculus
Calculus- Maclaurin series of integral sin(x)/x
Taylor Series and Maclaurin Series - Calculus 2
Maclaurin Series For Sin(x)
Maclaurin Series for sin(x)
Taylor series | Chapter 11, Essence of calculus
Find The Maclaurin Series Expansion For f(x) = sin x, a = 0
Taylor Series and Maclaurin Series - Calculus 2 || Maclaurin's series expansion of sinx ||Arya
Power series of sin(x) and cos(x) at 0
Maclaurin series of sin^2x
What is the Taylor series for sin x around zero? - Week 6 - Lecture 4 - Sequences and Series
Maclaurin series of sin x^2
Taylor & Maclaurin series for sinx
MacLaurin series for sin(x) and cos(x), and a Taylor series for 1/x.
Maclaurin series of sinx cosx
Taylor Series of sin(x) centered at x = pi/4 #calculus #calculushelp #mathematics
Expansion Of Sinx | Maclaurin series
The Proof of y=sin(x) Equaling its Maclaurin Series
Addition and Subtraction of Maclaurin Series
Комментарии
 0:05:51
0:05:51
 0:06:33
0:06:33
 0:11:26
0:11:26
 0:04:50
0:04:50
 0:05:20
0:05:20
 0:22:22
0:22:22
 0:07:06
0:07:06
 0:29:22
0:29:22
 0:10:02
0:10:02
 0:08:52
0:08:52
 0:22:20
0:22:20
 0:03:58
0:03:58
 0:12:23
0:12:23
 0:11:46
0:11:46
 0:17:24
0:17:24
 0:04:37
0:04:37
 0:05:34
0:05:34
 0:04:17
0:04:17
 0:13:22
0:13:22
 0:06:21
0:06:21
 0:00:51
0:00:51
 0:04:29
0:04:29
 0:06:27
0:06:27
 0:05:45
0:05:45