De Morgan's Laws (in a probability context)

Показать описание

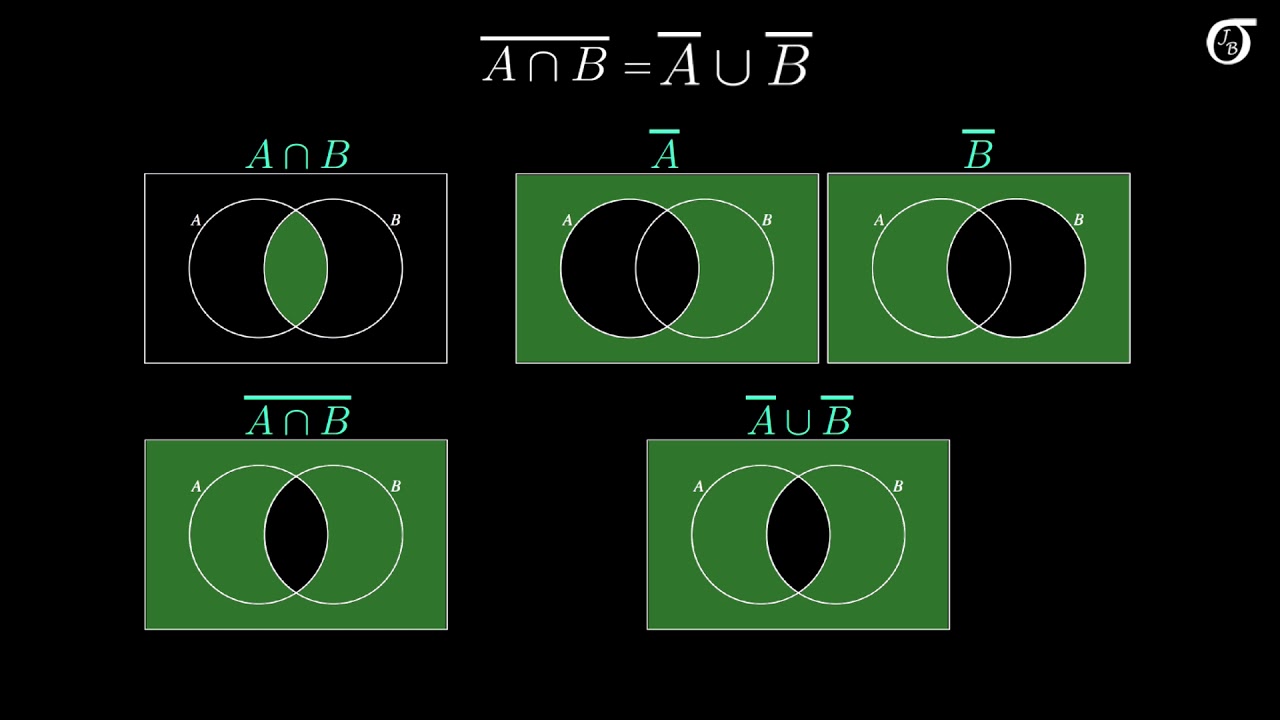
A discussion of De Morgan's laws, in the context of basic probability. I illustrate De Morgan's laws using Venn diagrams, describe their meaning in a worded example, and show how they might be useful in a probability calculation.

I will get back to statistics videos in the not-too-distant future. Right now, I'm hammering away on probability for a little while.

Рекомендации по теме

Комментарии

This one has seemed the most intuitive of this entire series to me

Cleisthenes

I really got over-stimulated by the name of job A

Francois

This was incredibly clear - thanks and great job.

regularfoodblog

This is the literal best explanation on the entire internet

melontusk

Thank you so much for your videos. I passed my probability class with a good grade because of you! (:

BattleFieldGalaxy

Clearly illustrated and explained. Thank you

ishitakothari

hands down one of the best explanations ive ever heard.
thank you for the examples

Cerealonmars

Study for AP computer science this year, this helps a lot, thank you!

ethanpan

These videos are very clear and useful. Great job! Now I have to go back and like them each individually...

ineriswetrust

amazing video :) literally so easy and simple to understand, thank you 🙏

veyshaliramathar

We Canadians are the best at everything! Well in this case you are Jb. Thanks man!

thedeathofbirth

thank you thank you, this was so helpful!

katiedunn

Thank you for this, really got the idea behind it after watching this!

marklendacky

You really know how to teach! Thank you!

amywilderson

Let's take it up a notch, because I have a problem that's more complicated. I have 10 digits, A through J, and from those I generate a 4-digit ordered string such as AAAA or ABCD or AJAE. I want to know the probability that the string has at least one A in it. Call the 4 variables that make up the string w, x, y, z, so the string is wxyz. We are then finding the probability of statement S:="w=A or x=A or y=A or z=A". I am not sure if this is correct, but I believe one way to proceed is to find the easier probability of not S = "w != A and x != A and y != A and z != A". The probability that w != A is (1-pr(w=A))=(1-0.1)=0.9, and the same for x, y, and z. Thus, we multiply the probabilities together so that the probability of not S is (0.9)^4 = 6561/10000, and thus the probability of S is (1-Pr(not So, the probability that at least one digit is an A is 0.3439. I believe this is correct. I don't know how to put this in the language of sets instead of the language of boolean statements.

wiggles