filmov
tv
Arc Length of a Polar Curve
Показать описание
This video explains how to determine the arc length of a polar curve.
Arc Length of Polar Curves
Arc Length of A Polar Curve (proof)
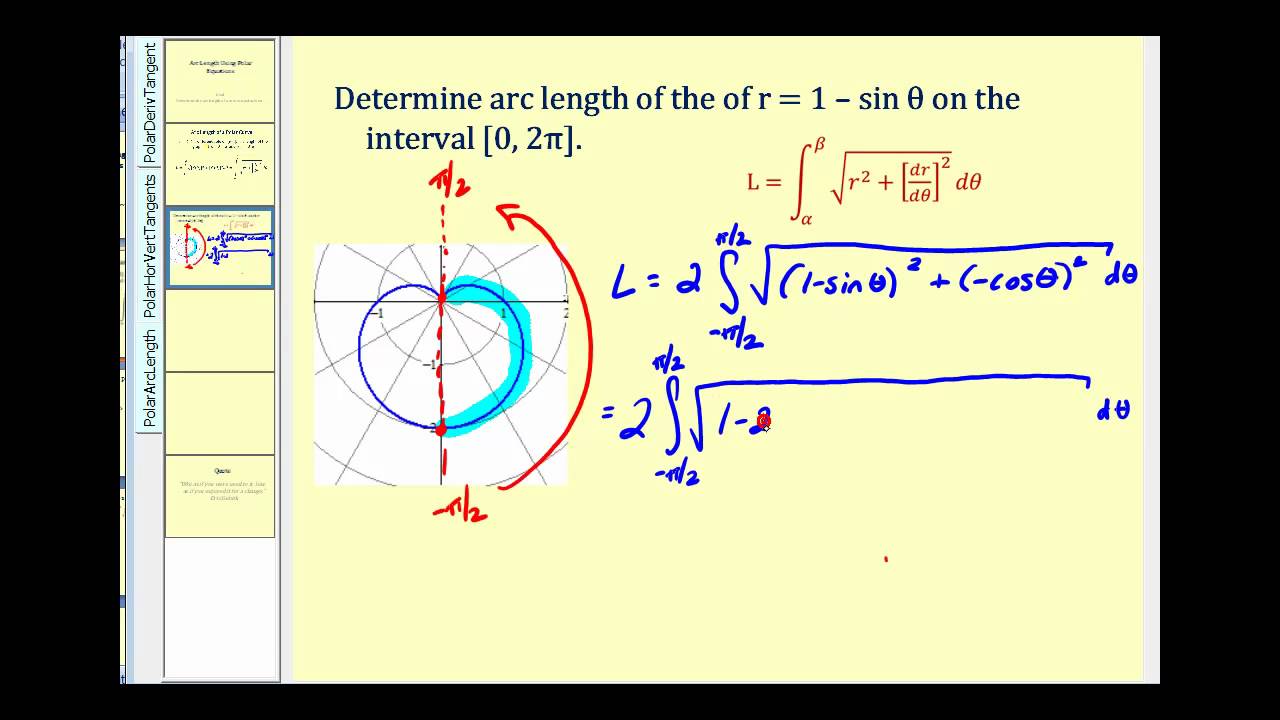
Arc Length of a Polar Curve
Ex 2: Arc Length of a Polar Curve
Arc Length of Polar Curves | Calculus 2 Lesson 51 - JK Math
Deriving the arc length of a Polar Equation in 4 minutes (with examples!)
POLAR ARC LENGTH
Arc Length of a Polar Curve (KristaKingMath)
[50] Arc Length in Calculus: Mastering Integration Techniques
Area and Arc Length for Polar Curves
Arc Length of a Polar Curve
Arc Length of a Cardioid! [ Using a Polar Coordinate System ]
Derivation and Example of Arc length for Polar Form of an Equation
Calculus-Finding Arc Length of Polar Curves
Polar Parametric Curve - Arc Length (KristaKingMath)
Arc length of polar curves
Arc length of petal of polar graph
Arc Length along Polar Curve r = e^{-O}
Areas and Arc Length in Polar Coordinates
Justification for polar arc length formula
Deriving the Arc Length in Cartesian and Polar Coordinates
Arc length of a polar curve (Integrals)
Finding the Arc Length of a Polar Curve
Arc Length in Polar Coordinates
Комментарии
 0:10:33
0:10:33
 0:08:11
0:08:11
 0:07:38
0:07:38
 0:07:34
0:07:34
 0:39:59
0:39:59
 0:04:09
0:04:09
 0:09:53
0:09:53
 0:07:56
0:07:56
![[50] Arc Length](https://i.ytimg.com/vi/N380VaPfDos/hqdefault.jpg) 0:17:49
0:17:49
 0:07:53
0:07:53
 0:05:01
0:05:01
 0:08:38
0:08:38
 0:06:28
0:06:28
 0:10:05
0:10:05
 0:07:04
0:07:04
 0:09:33
0:09:33
 0:06:23
0:06:23
 0:06:06
0:06:06
 0:41:16
0:41:16
 0:11:45
0:11:45
 0:13:48
0:13:48
 0:02:20
0:02:20
 0:09:18
0:09:18
 0:07:56
0:07:56