Electric field of a uniformly charged solid sphere using Gauss' Law (how to use Gauss' Law)

00:00 In this video, we compute the electric field of a uniformly charged solid sphere using Gauss' Law. We compute the electric field of a sphere inside and outside the sphere, we show the electric field is continuous at the surface of the sphere, and we plot the magnitude of the electric field as a function of distance from the center of the charged sphere.

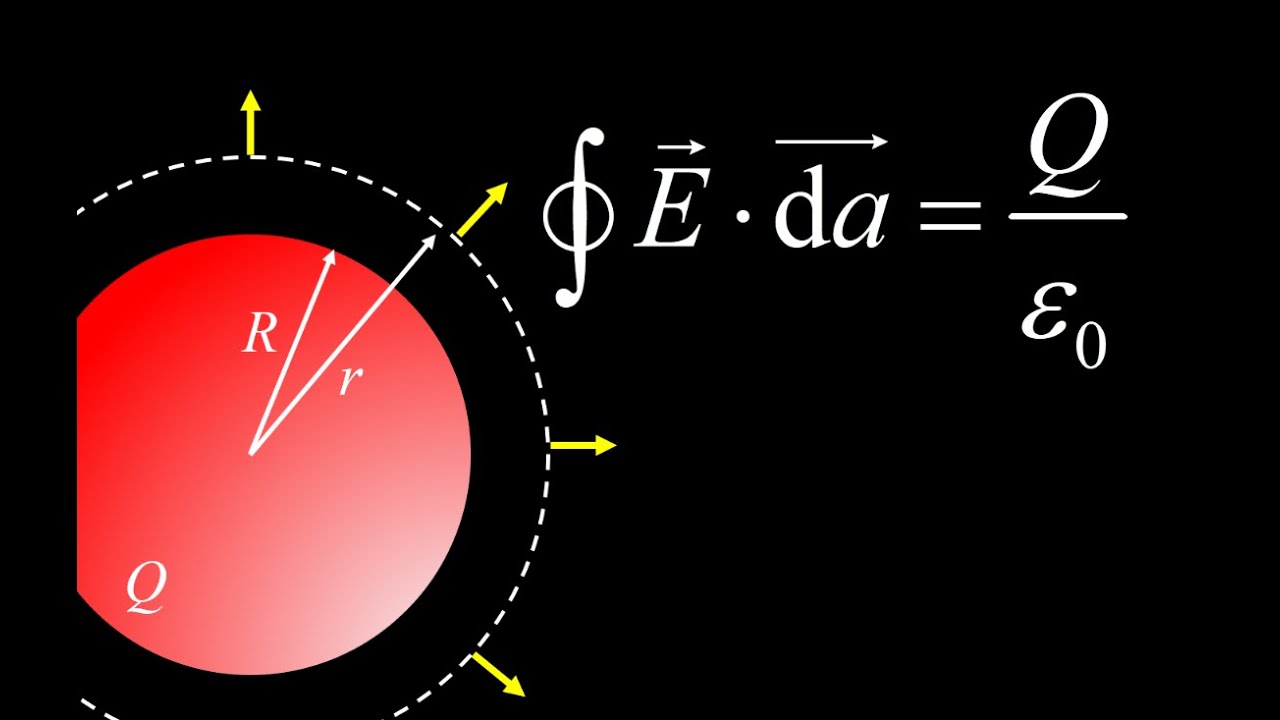
00:16 Electric field outside the sphere: we choose a Gaussian surface outside the sphere in order to compute the electric field outside the sphere. We compute the electric flux integral on the left side of Gauss' Law by taking advantage of the symmetry of the Gaussian surface: first, the electric field is parallel to the normal vector at every point along the Gaussian surface, and second, the electric field magnitude is constant over the entire Gaussian surface. The first property renders the dot product in the flux integral trivial, and the second property allows us to factor E out of the flux integral. We are left with an area integral equal to the surface area of the Gaussian surface.

02:28 Enclosed charge for the first Gaussian surface: the enclosed charge for the Gaussian surface outside the spherical charge distribution is just Q, the total charge on the sphere. Applying Gauss' Law and using our previous result for the electric flux integral, we arrive at the electric field outside the charged sphere, and it turns out to be the exact same thing as the electric field of a point charge located at the center of the sphere!

03:10 Electric field inside the sphere: now we use a Gaussian surface inside the solid spherical charge distribution. Once again, the symmetry of the Gaussian surface means the electric field is both parallel to the normal vector and constant in magnitude at every point along the surface, so the flux integral quickly simplifies to the electric field magnitude multiplied by the surface area of the Gaussian surface.

04:00 Enclosed charge for the second Gaussian surface: the enclosed charge is trickier for the Gaussian surface inside the charged sphere. We introduce the concept of volume charge density, and we compute the charge density of the sphere by taking the total charge Q for the sphere and dividing by its total volume 4/3*pi*R^3. Now the enclosed charge can be computed as charge density multiplied by the volume of the Gaussian sphere 4/3*pi*r^3. We apply Gauss' Law and arrive at the electric field inside the solid sphere, and it turns out to grow linearly with distance from the center!

05:50 Electric field is continuous at the surface and plot E(r): we show E is continuous at the surface of the uniformly charged sphere by substituting R for r in each equation for the electric field inside and outside the charged sphere. Finally, we make a plot of the electric field magnitude inside and outside the uniformly charged spherical charge distribution.

[PROJECTJoza]

Much better explained than in my script. Thanks!

[pajamaboy]

The viewer quantity certainly does not indicate the quality. The video was extremely helpful with clear visualizations, thank you.

[sarsax]

Amazing video! Exactly what i was looking for!

[noahskinner]

Fantastically crafted video. This really helped me with what I needed.

[Hirosuke]

Hi, I'm having difficulties with an exercise that has the same premise, but I need to find the difference in potential (ddp) between the center and r < R. Do you have any suggestions?

[bobthebuilder]

Hi for the electric field within a uniformly charge sphere, ik u used the volume charge density, but can i use the surface area charge density instead? i realise i did it using surface charge denisty and got a different answer, i got back q(enclosed)/e0

[LanoMusambazi-srmx]

The font is just too small to see clearly.