filmov
tv
Principal Component Analysis (PCA) [Matlab]

Показать описание
This video describes how the singular value decomposition (SVD) can be used for principal component analysis (PCA) in Matlab.
These lectures follow Chapter 1 from: "Data-Driven Science and Engineering: Machine Learning, Dynamical Systems, and Control" by Brunton and Kutz
This video was produced at the University of Washington
These lectures follow Chapter 1 from: "Data-Driven Science and Engineering: Machine Learning, Dynamical Systems, and Control" by Brunton and Kutz
This video was produced at the University of Washington
Principal Component Analysis (PCA) | MATLAB | Machine Learning
Principal Component Analysis (PCA) using MATLAB | MATLAB Tutorial for Beginners | Simplilearn
Principal Component Analysis (PCA) [Matlab]
Doing Principal Components Analysis in Matlab - using the pca function (Statistics Toolbox)
Principal Component Analysis in MATLAB
PCA in matlab ( Principal Component analysis in Matlab)
Calculating Principal component analysis (PCA), step by step using a simple dataset.
Principal Component Analysis (PCA)
Principal Component Analysis (PCA) in MATLAB
Principal Component Analysis (PCA) - easy and practical explanation
StatQuest: PCA main ideas in only 5 minutes!!!
Principle Component Analysis Matlab Tutorial Part 1 - Overview
MATLAB tutorial - principal component analysis (PCA)
Principal Component Analysis (PCA) in Python and MATLAB
MATLAB CODE for FACE RECOGNITION using Principal Component Analysis PCA
Face recognition using Principal Component Analysis(PCA) in Matlab - Part 2.2( II )
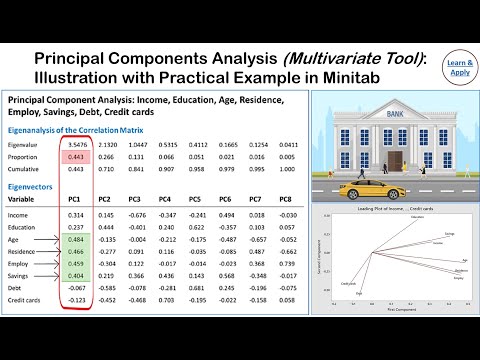
Principal Component Analysis (PCA): With Practical Example in Minitab
Understand & interpret result of pca MATLAB | Machine Learning
Principal Component Analysis - Theory & MATLAB Implementation | Machine Learning | @MATLABHelper
Data Analysis 6: Principal Component Analysis (PCA) - Computerphile
MATLAB tutorial: Principal Component Analysis & Regression
Principal Component Analysis (PCA) Intuition | Machine Learning
Principal Component Analysis- Part I
PCA using MATLAB: Simplify Data Insights #PCA #matlabtutorial
Комментарии
 0:09:21
0:09:21
 0:34:19
0:34:19
 0:15:56
0:15:56
 0:05:24
0:05:24
 0:05:33
0:05:33
 0:04:00
0:04:00
 0:21:22
0:21:22
 0:13:46
0:13:46
 0:10:09
0:10:09
 0:10:56
0:10:56
 0:06:05
0:06:05
 0:03:11
0:03:11
 0:05:25
0:05:25
 1:20:08
1:20:08
 0:00:56
0:00:56
 0:03:11
0:03:11
 0:09:36
0:09:36
 0:09:27
0:09:27
 0:06:32
0:06:32
 0:20:09
0:20:09
 0:12:18
0:12:18
 0:13:40
0:13:40
 0:13:41
0:13:41
 0:02:36
0:02:36