filmov
tv
Log Tables - Numberphile

Показать описание
Logarithms and log tables - what Professor Bowley used before calculators!
More links & stuff in full description below ↓↓↓
Professor Roger Bowley is an emeritus professor at the University of Nottingham.
NUMBERPHILE
Videos by Brady Haran
More links & stuff in full description below ↓↓↓
Professor Roger Bowley is an emeritus professor at the University of Nottingham.
NUMBERPHILE
Videos by Brady Haran
Log Tables - Numberphile
Log Tables (extra bit) - Numberphile
Logarithms, Explained - Steve Kelly
Logarithms: why do they even exist?
The History of the Natural Logarithm - How was it discovered?
Logarithms: What problem was Napier trying to solve?
Fix a Wobbly Table (with Math)
Elliptical Pool Table - Numberphile
LOGARITHM OF NUMBERS USING LOG TABLE | FRENCH SUBTITLE@freemathsvideos
The Slightly Spooky Recamán Sequence - Numberphile
How to make railway timetables (with graphs) - Numberphile
A Sequence with a Mistake - Numberphile
How We Used Log Tables
Partitions - Numberphile
The Last Digit of Prime Numbers - Numberphile
The Graceful Tree Problem - Numberphile
The 8 Queen Problem - Numberphile
2.920050977316 - Numberphile
A proof that e is irrational - Numberphile
Look-and-Say Numbers (feat John Conway) - Numberphile
Happy Ending Problem - Numberphile
The Neverending Story (and Droste Effect) - Numberphile
How people came up with the natural logarithm and the exponential function #SoME1
The Key to the Riemann Hypothesis - Numberphile
Комментарии
 0:05:10
0:05:10
 0:05:44
0:05:44
 0:03:34
0:03:34
 0:12:47
0:12:47
 0:18:21
0:18:21
 0:05:45
0:05:45
 0:07:22
0:07:22
 0:03:40
0:03:40
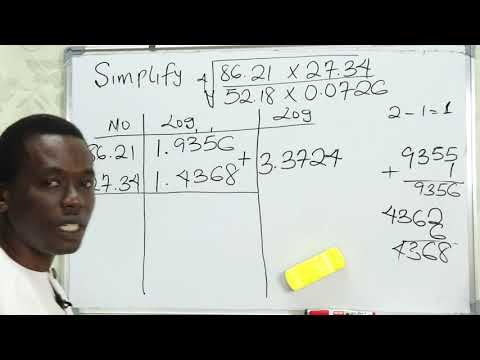 0:13:39
0:13:39
 0:10:05
0:10:05
 0:08:43
0:08:43
 0:03:21
0:03:21
 0:29:12
0:29:12
 0:11:45
0:11:45
 0:09:44
0:09:44
 0:09:59
0:09:59
 0:07:04
0:07:04
 0:12:42
0:12:42
 0:16:29
0:16:29
 0:07:53
0:07:53
 0:05:05
0:05:05
 0:06:23
0:06:23
 0:33:25
0:33:25
 0:12:38
0:12:38