filmov
tv
Multivariable calculus, class #8: Linearization, the Jacobian, and higher-order partial derivatives

Показать описание
Mathematician spotlight: Ryan Hynd
We review the idea of linear approximation (tangent plane) for functions from R^2 to R, now writing it in vector form, and define the gradient. We then extend the notion of best linear approximation to functions from R^m to R^n, and define the Jacobian matrix. We do an example. Finally, we take all four second partial derivatives of a function of two variables, and state and discuss Clairaut's Theorem.
We review the idea of linear approximation (tangent plane) for functions from R^2 to R, now writing it in vector form, and define the gradient. We then extend the notion of best linear approximation to functions from R^m to R^n, and define the Jacobian matrix. We do an example. Finally, we take all four second partial derivatives of a function of two variables, and state and discuss Clairaut's Theorem.
Multivariable calculus, class #8: Linearization, the Jacobian, and higher-order partial derivatives
14.4 Linearization of a multi-variable function
Differentials and linearization in Multivariable Calculus
three-variable linearization
Multivariable Calculus Unit 10: Linearization
Linearization of f(x, y) = e^xcos(xy) at (0,0)
Find Linear approximation (linearization) of f at the point
Another Multivariable Linearization
🟡11 - Linearization (Linear Approximation) of Multivariable Functions
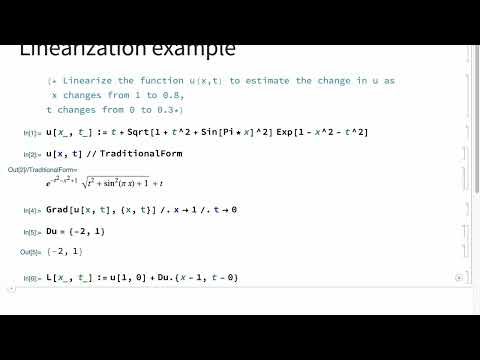
Linearization in Mathematica, Multivariable Calculus
Finding Linearization in Two Variables and Error Bound
How to Distinguish Between Linear & Nonlinear : Math Teacher Tips
M4ML - Multivariate Calculus - 4.8 Multivariate Taylor
Class 25: Linearization
Finding Linearisation
Linearization of a vector-valued function
What is linear approximation?
CalcBLUE 2 : Ch. 11.1 : Linearization and Differentials
3.10.1 Find Linear Approximation (Linearization)
Electronics basics: Linearization of multivariable function and SPICE
Multivariable Calculus: Tangent Planes and Linearization (14.4)
CASS 37 5B08MAT VECTOR CALCULUS MODULE II Linearization, Standard Linear Approximation and Error in
14.4: Tangent Planes and Linear Approximations (1/2)
Log Linearization in an RBC Model
Комментарии
 0:08:43
0:08:43
 0:06:50
0:06:50
 0:02:02
0:02:02
 0:18:46
0:18:46
 0:04:26
0:04:26
 0:06:34
0:06:34
 0:06:14
0:06:14
 0:11:09
0:11:09
 0:04:43
0:04:43
 0:08:40
0:08:40
 0:01:57
0:01:57
 0:06:28
0:06:28
 0:13:06
0:13:06
 0:07:26
0:07:26
 0:05:13
0:05:13
 0:08:57
0:08:57
 0:03:31
0:03:31
 0:17:12
0:17:12
 0:25:33
0:25:33
 0:27:38
0:27:38
 0:12:47
0:12:47
 0:39:55
0:39:55
 0:04:15
0:04:15