Tensor Calculus Lecture 15: Geodesic Curvature Preview

Rules of the Game
Coordinate Systems and the Role of Tensor Calculus
Change of Coordinates
The Tensor Description of Euclidean Spaces
The Tensor Property
Elements of Linear Algebra in Tensor Notation
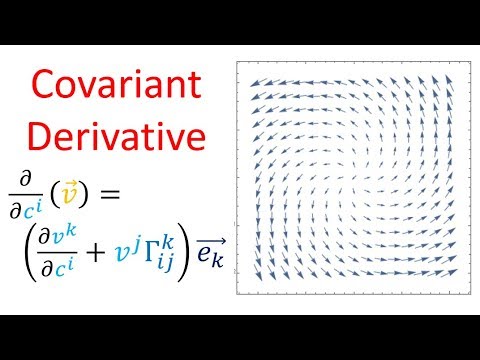
Covariant Differentiation
Determinants and the Levi-Civita Symbol
The Tensor Description of Embedded Surfaces
The Covariant Surface Derivative
Curvature
Embedded Curves
Integration and Gauss’s Theorem
The Foundations of the Calculus of Moving Surfaces
Extension to Arbitrary Tensors
Applications of the Calculus of Moving Surfaces

Index:
Absolute tensor
Affine coordinates
Arc length
Beltrami operator
Bianchi identities
Binormal of a curve
Cartesian coordinates
Christoffel symbol
Codazzi equation
Contraction theorem
Contravaraint metric tensor
Contravariant basis
Contravariant components
Contravariant metric tensor
Coordinate basis
Covariant basis
Covariant derivative
Metrinilic property
Covariant metric tensor
Covariant tensor
Curl
Curvature normal
Curvature tensor
Cuvature of a curve
Cylindrical axis
Cylindrical coordinates
Delta systems
Differentiation of vector fields
Directional derivative
Dirichlet boundary condition
Divergence
Divergence theorem
Dummy index
Einstein summation convention
Einstein tensor
Equation of a geodesic
Euclidean space
Extrinsic curvature tensor
First groundform
Fluid film equations
Frenet formulas
Gauss’s theorem
Gauss’s Theorema Egregium
Gauss–Bonnet theorem
Gauss–Codazzi equation
Gaussian curvature
Genus of a closed surface
Geodesic
Gradient
Index juggling
Inner product matrix
Intrinsic derivative
Invariant
Invariant time derivative
Jolt of a particle
Kronecker symbol
Levi-Civita symbol
Mean curvature
Metric tensor
Metrics
Minimal surface
Normal derivative
Normal velocity
Orientation of a coordinate system
Orientation preserving coordinate change
Relative invariant
Relative tensor
Repeated index
Ricci tensor
Riemann space
Riemann–Christoffel tensor
Scalar
Scalar curvature
Second groundform
Shift tensor
Stokes’ theorem
Surface divergence
Surface Laplacian
Surge of a particle
Tangential coordinate velocity
Tensor property
Theorema Egregium
Third groundform
Thomas formula
Time evolution of integrals
Torsion of a curve
Total curvature
Variant
Vector
Parallelism along a curve
Permutation symbol
Polar coordinates
Position vector
Principal curvatures
Principal normal
Quotient theorem
Radius vector
Rayleigh quotient
Rectilinear coordinates
Vector curvature normal
Vector curvature tensor
Velocity of an interface
Volume element
Voss–Weyl formula
Weingarten’s formula

Applications: Differenital Geometry, Relativity

[MaxwellsWitch]

I want to thank you for these videos Professor Grinfeld. I discovered your tensor calculus videos when I was merely in calc 3, actually around the time you were publishing these videos too. I didn't understand it much at the time, and had no idea where to use what these videos taught. I took electrodynamics over a year ago, almost forgetting your series. I was trying to understand and generalize transformations between coordinate systems, length would pop out of the Jacobian, giving dimensional length to the basis vectors. My calc 3 class didn't touch the Jacobian, or coordinate transformations. I binge watched your series again last summer, and I could understand it all in it's beauty. Your lectures were filled with meaning and binding the geometry and algebra in a very elegant way. It was hard to get bored watching as every episode had something profound I probably would never have found myself. Last semester I decided to take a class in Relativity, and tensors are heavily used in that class. I would always finish the problem sets and exams so easily it felt like cheating. All because the thought and meaning behind the symbols I learned from your series. I am taking a graduate class in general relativity this semester, and what you have taught me about geometry and tensor calculus has been invaluable to me. I am a double major in Electrical Engineering and Physics, and sometimes I wonder if I should have done math instead. Anyways, thank you so much for making these videos! Perhaps even that last sentence is an understatement of my gratitude.

[happyhayot]

Couldn't describe with words what an amazing contribution this is to all of us who love to learn. Grateful is an understatement. I still have much to learn, but this really puts me in the right track. Thank you professor.

[SupBroLetsChill]

PLEASE don't this lecture series die professor. Looking forward to more.

[rxdsza]

I've finally completed your book and wanted to leave a word of thanks here!

I come from a Physics background and wasn't expecting to get far into a course on tensors taught by a mathematician but your geometric approach and insights made these ideas very digestable. Now when I look on the sections on Tensors in some books on Relativity, I realize how much better your approach is. The treatment of Tensors in Physics books isn't grounded & makes things feel like its something exotic. I remember having a similar experience when I first encountered Linear Algebra, my prof at the time ( a mathematician) said that its best to leave teaching math to the math dept. He was definitely on to something 😂.

Do you have any reccomendations for books that follow your style of teaching for Differential Geometry? If yes, I would love to have a go at it!

[IvanPavlov]

Yay, made it! Huge thanks to you, Dr. Grinfeld! Your explanations in this series restored my faith in simple intuition and derivations, something I (sadly) last encountered many years ago with my precalc teacher. I'm a 4th year engineering student, and like some of these folk as well am looking forwards to getting into general relativity and topology. I found your book in our library - I wish more books were written like this.

Can't wait for CMS :) Thanks again a bunch.

[muldermachines]

Hi Pavel. Your book and video series has been very useful for me. I second the request for videos on the remainder of your book (when you get time). Thanks!

[Crandog]

Great lecture series, thank you. Your passion for geometric intuition is contagious, and your energy and timing as a teacher is infallible. Very much looking forward to a follow up series on the calculus of moving surfaces!

[redotto]

I too hope you decide to make more videos covering part 3 of your book. You are very articulate and make learning the subject a lot of fun!

[georgeorourke]

Beautiful lectures that are really very clear (although I had to listen to the entire set three times before I fully appreciated the richness of the subject). It is a real priviledge to be able to have access to to such great material. Thank you very much and I do hope that a follow-up on moving surfaces is "in the works".

[englemanart]

Just a great series. Will watch the whole thing again.

[marxman]

Thank you Professor Grinfeld. Hope more videos coming from you. Tensor calculus is a very difficult subject, but your teaching was a lot of fun, really amazing.

[emanuelesiego]

I've just completed the lectures and now I'm going to complete the last part of the book. Awesome: it's the perfect combination of rigor and practical intuition. I hope in a new book on differential geometry in order to see the other side of the coin. Are you going to write it? Thank you for your precious work!

[johnstroughair]

Great series! Where can I find the follow on videos?

[alexbenjamin]

Any relation to the use of parallel transport to define geodesics?

[menturinai]

With your apple example, I can visualize the shortest curve connecting two points having curvature normal aligned with the surface normal N along the path. However, if there is a cut in the surface of the apple, in order to get around this, I would imagine there would have to be an in-plane component along the new shortest path. Does the surface have to be closed to have no in-plane components?

[adriangheorghe]

Care sunt dimensiunile fizice ale tensorilor? in LMT sau in m, Kg, s.

What are the physical dimensions of tensors? in LMT or in m, Kg, s.

[adriangheorghe]

Va rog doar sa imi confirmati daca aceste dimensiuni, ale termenilor din ecuatia de camp, gasite pe internet, sunt corecte sau sunt gresite.
[G(miu, niu)]=M.L^-1.T^-2; [R]=[Lamda]=L^-2; [g(miu, niu)]=M.L.T^-2; [T(miu, niu)]=M^2.T^-4. Si daca cu aceste dimensiuni ale tensorilor si curburilor din ecuatia de camp se verifica omogenitatea dimensionala a ecuatiei relativiste a gravitatiei?

Please just confirm if these dimensions, of the terms in the field equation, found on the internet, are correct or wrong.
[G(miu, niu)]=M.L^-1.T^-2; [R]=[Lamda]=L^-2; [g(miu, niu)]=M.L.T^-2; [T(miu, niu)]=M^2.T^-4. And if the dimensional homogeneity of the relativistic gravity equation is checked with these dimensions of the tensors and curves in the field equation?

[AshishPatel-yqxc]

Hi. Will you be adding lectures to cover part 3 of the book on CMS ?

[sufyannaeem]

is that the end of the series??? or i am missing something???

[adriangheorghe]

Thank you for being kind enough to answer me. but your answer doesn't help me at all. I am interested in receiving the physical dimensions of all the terms in Einstein's field equation and curves and tensors, in L, M, T,
or in m, Kg, s, to check if the equation is dimensionally homogeneous. Because in all the articles with the field equation or the relativistic equation of gravity, these dimensions are never given. They say that they are energies, that they are impulses, that they are forces, that they are pressures, that they are densities of energy, impulses or forces. What is the truth? What kind of equation is the field equation?