filmov
tv
Tensor Calculus 16: Geodesic Examples on Plane and Sphere

Показать описание
Tensor Calculus 16: Geodesic Examples on Plane and Sphere
Tensor Calculus 15: Geodesics and Christoffel Symbols (extrinsic geometry)
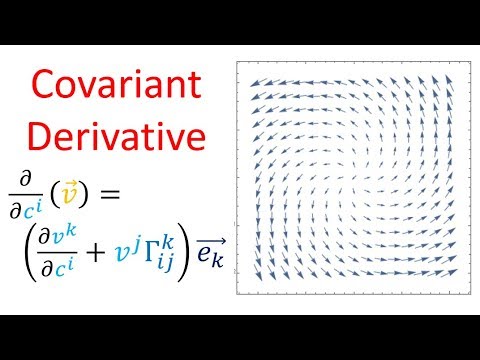
Tensor Calculus 17: The Covariant Derivative (flat space)
Relating Metric Tensor to Gravity | Tensor Calculus Ep. 16
Tensor Calculus 19: Covariant Derivative (Intrinsic) and Geodesics
Tensor Calculus 22: Riemann Curvature Tensor Geometric Meaning (Holonomy + Geodesic Deviation)
Tensor Calculus 18: Covariant Derivative (extrinsic) and Parallel Transport
Tensors for Beginners 16: Raising/Lowering Indexes (with motivation, sharp + flat operators)
Tensor Calculus 6: Differential Forms are Covectors
Conceptualizing the Christoffel Symbols: An Adventure in Curvilinear Coordinates
Relativity 107b: General Relativity Basics - Manifolds, Covariant Derivative, Geodesics
Metric Tensor & Geodesic distance | Tensor Analysis
Tensor Calculus 13: Gradient vs 'd' operator (exterior derivative/differential)
Tensor Calculus 14: Gradient explanation + examples
Tensor Calculus 0: Introduction
Tensor Calculus for Engineers and Physicists
Solving the Geodesic Equation for Cartesian Space
Tensor Calculus 1: Multi-variable Calculus Review (Updated with correction)
geodesic equation
Tensor Calculus Lecture 7b: Relative Tensors
Tensor Analysis, Lec.-13(Edition Version)(Geodesic and differential equation of Geodesic)
Tensor Calculus 12: The Metric Tensor in Curved Spaces for Measuring Arc Length
Ling Ling teaches you General Relativity: Geodesic Deviation
Tensor Calculus 17.5: Covariant Derivative (Component Definition) - Optional
Комментарии
 0:20:55
0:20:55
 0:21:40
0:21:40
 0:18:12
0:18:12
 0:19:05
0:19:05
 0:22:50
0:22:50
 0:29:13
0:29:13
 0:33:51
0:33:51
 0:15:44
0:15:44
 0:15:49
0:15:49
 0:23:38
0:23:38
 0:36:21
0:36:21
 0:18:03
0:18:03
 0:19:07
0:19:07
 0:14:40
0:14:40
 0:12:43
0:12:43
 0:01:18
0:01:18
 0:11:17
0:11:17
 0:17:09
0:17:09
 0:04:43
0:04:43
 0:18:02
0:18:02
 0:26:39
0:26:39
 0:23:09
0:23:09
 0:10:29
0:10:29
 0:16:50
0:16:50