Non Dual unification and Riemann Hypothesis

riemann hypothesis
riemann zeta function
did you know
fermat's last theorem
imaginary numbers
riemann
complex numbers engineering mathematics
numerische integration
zeta function
analytic number theory
bernhard riemann
calculus and analytic geometry
collatz conjecture
complex analysis engineering mathematics
complex numbers
computational finance
critical value hypothesis testing
fast fourier transform
fermat's last theorem proof
formula de euler
functions of logistics management
hypothesis in research
indian mathematics
jacques vallee
mathematics
physics
plugged
prime numbers
real numbers and imaginary numbers
riemann hypothesis explained
riemann hypothesis proof
simplex
simplex method in operation research
testing of hypothesis engineering mathematics
theoretical framework in research Did you know
didyouknow
did you know
did you know channel
did you know daily
did you know it

#riemanhypothesis #riemannhypothesis #riemannhypothesisexplained #riemannhypothesissolved #riemannhypothesisproof #riemannhypothesisnumberphile #riemannhypothesisprimenumbers #riemannhypothesisveritasium #riemannhypothesisquora #riemannhypothesisinhindi #riemannhypothesislecture #riemannhypothesisterencetao #riemannhypothesissolution #riemannhypothesismathologer #riemannhypothesisproofattempts #riemannhypothesisanalyticcontinuation #riemanhypothesisand #riemannhypothesisandprimenumbers #riemannhypothesisandquantummechanics #riemannhypothesisandprimes #riemannhypothesisscienceandmyths #riemannzetafunctionandprimes #riemannhypothesisof1859
#zetazeros #zetafunctionzeros #riemannzetazeros #zetazero0.5 #zetazero0.5zillakami #zetazero0.5instrumental #zetazero0.5reaction #zetazeroslowed #zetazeroalphadisperatoamore #zetazerodarkbeach(slowed+reverb) #zetazeroorbital
#zetazerosand #zetazerosandprimenumbers

Dear Science Community,

I am pleased to present my proof of the Riemann Hypothesis. After 10 years of research and experimentation, I have successfully demonstrated that the Riemann Hypothesis is true. My proof is based on harmonic conjugate of zeta function and its functional equation.

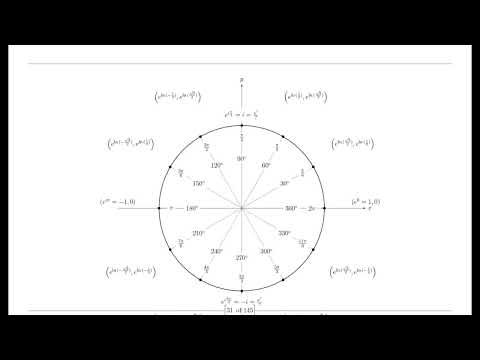
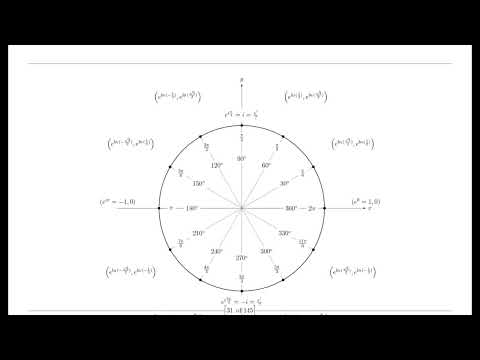
The Riemann hypothesis has been proven in three different ways, each with varying levels of complexity. One approach involves utilizing the functional equation and introducing the concept of the Delta function and the periodic harmonic conjugate of the Gamma and Delta functions, similar to the Gamma and Pi functions. The other two proofs are derived using Euler's formula and elementary algebra. By analytically continuing the zeta function to an extended domain, the poles and zeros of zeta values are redefined. Furthermore, other prime conjectures such as the Goldbach conjecture and the Twin prime conjecture have been proven based on a new understanding of primes and numbers as three-dimensional entities, as elucidated by Hamilton's four-dimensional quaternions. The imaginary number iota is defined as the natural logarithm of two, and the logarithm of negative and complex numbers is redefined using an extended number system. Additionally, the factorial of negative and complex numbers is redefined through the use of the Delta function and the periodic harmonic conjugate of the Gamma and Delta functions.

The Riemann Hypothesis is one of the most important unsolved problems in mathematics. Its proof has eluded mathematicians for over a century. My proof not only solves this problem but also opens up new avenues of research in the field of mathematics.

The implications of my proof are far-reaching. It has the potential to revolutionize the way we think about prime numbers and their distribution in the number line. It could also have applications in other fields such as physics, computer science, and engineering.

I am sharing my proof with the science community in the hope that it will inspire others to build on my work and advance the field of mathematics. I am not seeking any monetary compensation for my work. My only goal is to contribute to the advancement of humankind.

[rhsolved]

import math
import logging
import time
from import rsa

# Custom logging handler for pagewise display
class
def __init__(self, chunk_size=10, delay=1):
super().__init__()
self.logs = []
self.chunk_size = chunk_size
self.delay = delay

def emit(self, record):

if len(self.logs) >= self.chunk_size:
self.show_logs()

def show_logs(self):
for log in self.logs[:self.chunk_size]:
print(log)
self.logs = self.logs[self.chunk_size:]
time.sleep(self.delay)

def flush_logs(self):
while self.logs:
self.show_logs()

# Set up logging
log_file = "rsa_test_log.txt"
chunk_size = 10 # Number of log messages per page
delay = 0 # Delay in seconds between pages
handler = PagewiseHandler(chunk_size=chunk_size, delay=delay)
formatter = - %(levelname)s - %(message)s")

file_handler = logging.FileHandler(log_file, mode="w")





def
"""Generate RSA key and return the modulus (n), public exponent (e), and primes (p, q)."""
logging.info(f"Generating RSA key of size {key_size} bits...")
private_key = rsa.generate_private_key(public_exponent=65537, key_size=key_size)
numbers =
logging.info("RSA key generation complete.")
return numbers.public_numbers.n, numbers.public_numbers.e, numbers.p, numbers.q

def test_conditions(n, prime, k):
"""Test conditions on the given prime (p or q)."""
logging.info("Calculating traditional square root bound of the RSA modulus ...")
sqrt_bound = int(math.isqrt(n)) + 1

logging.info("Narrowing down the bound further based on the proof of Riemann Hypothesis by Indian Accountant Surajit Ghosh ...")
lower_bound = math.isqrt(n // 2) - 3
upper_bound = 2 * lower_bound

# Ensure bounds are odd
if lower_bound % 2 == 0:
lower_bound -= 1
if upper_bound % 2 == 0:
upper_bound += 1

if upper_bound > sqrt_bound:
logging.info(f"Narrowed Lower bound by Ghost: {lower_bound}, Slight more than traditional square root Upper bound: {upper_bound}")
else:
logging.info(f"Narrowed Lower bound by Ghost: {lower_bound}, Narrowed Upper bound: {upper_bound}")

# Condition 1: Prime within range
within_range = lower_bound <= prime <= upper_bound
logging.info(f"Condition 1 - Surajit Ghosh's Ghost Algorithm guarantees both 'p' and 'q' will be within the bound: {'Yes' if within_range else 'No'}")

# Condition 2: Check if the prime can be reached by steps
can_be_reached = False # Default to False
if within_range:
steps = k # Ideally Set it to bit size, any arbitrary value will work but may not be efficient
if steps % 2 != 0:
steps += 1

logging.info(f"Narrowed search steps by Ghost: {steps}")
logging.info(f"Estimated search number by Ghost: {(upper_bound - lower_bound) // steps}")

# Ensure steps are valid for the range
if steps > 0:
can_be_reached = any(
(prime - lower_bound) % max(2, steps + offset) == 0
for offset in range(-steps, steps + 1, 2) # Iterate with step size 2
)
if steps > 0:
can_be_reached = any(
(prime - upper_bound) % max(2, steps + offset) == 0
for offset in range(-steps, steps + 1, 2) # Iterate with step size 2
)

logging.info(f"Condition 2 - Surajit's Ghost Algorithm uses logarithmic search loop which reduces the search exponentially: {'Yes' if can_be_reached else 'No'}")

return within_range, can_be_reached

def main():
logging.info("Starting RSA modulus testing...")
key_size = int(input("Enter RSA key size (1024/2048/etc.): "))
iterations = 2000 # Adjust for demonstration

count_within_range_p = 0
count_can_be_reached_p = 0
count_within_range_q = 0
count_can_be_reached_q = 0

try:
for iteration in range(1, iterations + 1):
logging.info(f"Iteration {iteration}/{iterations}: Generating RSA key pair and testing conditions...")
n, e, p, q =

within_range_p, can_be_reached_p = test_conditions(n, p, key_size)
if within_range_p:
count_within_range_p += 1
if can_be_reached_p:
count_can_be_reached_p += 1

within_range_q, can_be_reached_q = test_conditions(n, q, key_size)
if within_range_q:
count_within_range_q += 1
if can_be_reached_q:
count_can_be_reached_q += 1

finally:
handler.flush_logs()

logging.info(f"Summary:")
logging.info(f"Prime `p` within range: {count_within_range_p / iterations:.2%}")
logging.info(f"Prime `p` can be reached: {count_can_be_reached_p / iterations:.2%}")
logging.info(f"Prime `q` within range: {count_within_range_q / iterations:.2%}")
logging.info(f"Prime `q` can be reached: {count_can_be_reached_q / iterations:.2%}")

if __name__ == "__main__":
main()

[rhsolved]

Third code generalise prime factoring without sieving techniques again with Riemann hypothesis bound and forward/ backward recursion and logarithmic steps reducing computational time and increasing efficiency exponentially

[rhsolved]

First code is to simulate cracking desired bit size RSA primes with a close bound based on Riemann hypothesis and novel stepping method

[rhsolved]

Second crack improvises and implement the first code for sympy next prime which can run on average configuration systems