filmov
tv
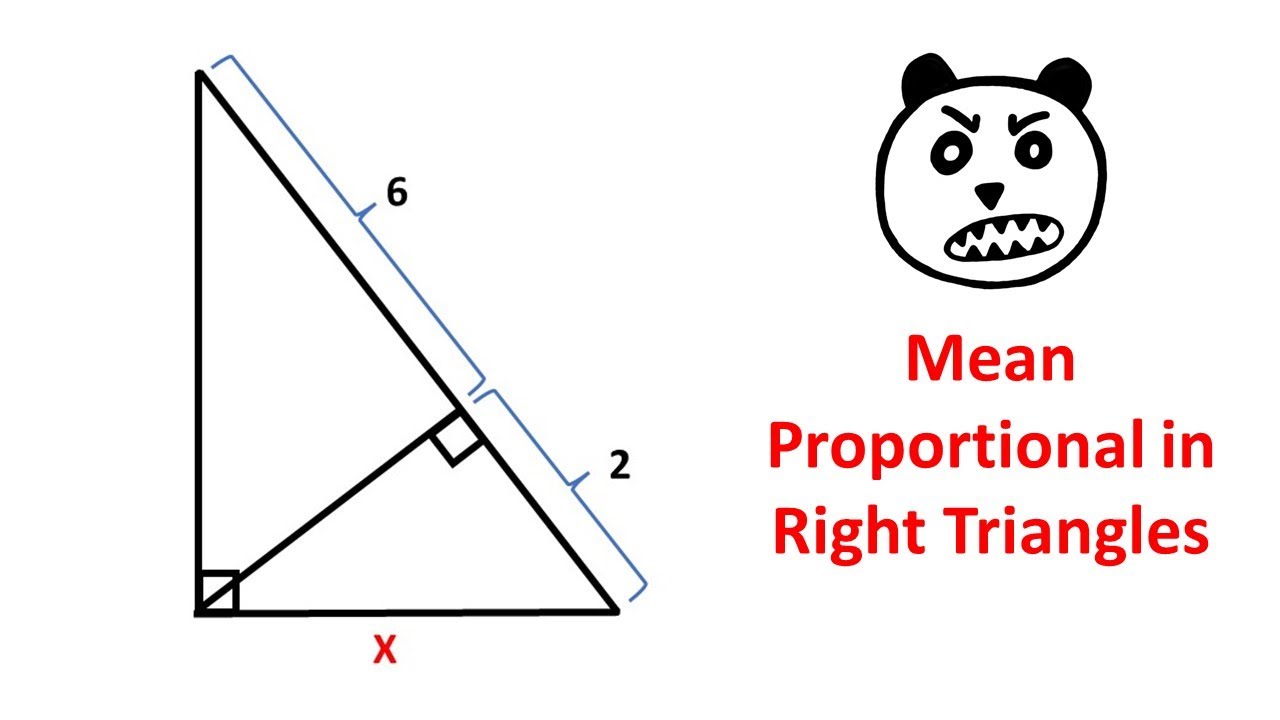
Mean Proportional in Right Triangles. Geometry video.
Показать описание
Leg rule proof. Right triangle properties.
#geometry #righttriangles #proportions
#geometry #righttriangles #proportions
Mean Proportional in Right Triangles. Geometry video.
Geometric Mean Theorems Altitude and Leg
Altitude to the Hypotenuse of a right triangle (Mean Proportional)
Similarity in Right Triangles - Geometric Mean Shortcut
Using the geometric mean to determine the missing parts of a triangle
Altitude Rule for Right Triangles - Geometry
Geometry - Basic Terminology (22 of 36) Proportions of the Right Triangle
Similarity, Right Triangles, & Trigonometry: Geometric Mean (1)
Right Triangle Proportions (HLLS and SAAS)
Altitude on Hypotenuse of Right Triangle - Geometric Means Theorem
Geometry Lesson 7.4 Similarity in Right Triangles
Proportions in the Right Triangle - Geometry
Geometric Mean in Right Triangles
Geometric Mean & Similar Right Triangles
Geometry Lesson 7.4: Similarity in Right Triangles
Similar Right Triangles: Geometric Mean (Altitude) Theorem
Geometry Lessons 4.9 & 4.10 Proportional Segments in Right Triangles
similarity in right triangles (geometry)
Altitude Geometric Mean Theorem
Geometric Mean in Right Triangles | High School Geometry Lesson
Altitude on Hypotenuse Theorem - Geometry Practice Problems
Triangles: Similar Right Triangles, Geometric Mean
Altitude Rule and Leg Rule in Right Triangles (Definition, Proof); Geometric mean, Mean proportional
Geometric Mean: Similarity in Right Triangles Jan 10
Комментарии
 0:02:07
0:02:07
 0:12:39
0:12:39
 0:20:35
0:20:35
 0:07:09
0:07:09
 0:06:42
0:06:42
 0:03:57
0:03:57
 0:04:03
0:04:03
 0:04:29
0:04:29
 0:07:44
0:07:44
 0:11:03
0:11:03
 0:08:02
0:08:02
 0:05:02
0:05:02
 0:03:39
0:03:39
 0:10:47
0:10:47
 0:16:06
0:16:06
 0:00:30
0:00:30
 0:16:25
0:16:25
 0:08:29
0:08:29
 0:03:12
0:03:12
 0:12:08
0:12:08
 0:24:50
0:24:50
 0:16:19
0:16:19
 0:11:58
0:11:58
 0:15:05
0:15:05