filmov
tv
Recurrence Relations: Recursion Tree Method

Показать описание
To solve recurrence relations, expanding the recursion tree can be used to either get an educated guess to use with the substitution method, or to directly prove a solution using induction.
Table of Contents:
00:00 - Introduction and Prerequisites
00:13 - Linear Search Example: T(n) = T(n-1) + 1
01:50 - Substitution Required?
02:31 - Inductive Proof (Skipping Substitution)
03:16 - MergeSort Example: T(n) = 2T(n/2) + n
04:35 - Why Substitution
05:26 - What's Next
Table of Contents:
00:00 - Introduction and Prerequisites
00:13 - Linear Search Example: T(n) = T(n-1) + 1
01:50 - Substitution Required?
02:31 - Inductive Proof (Skipping Substitution)
03:16 - MergeSort Example: T(n) = 2T(n/2) + n
04:35 - Why Substitution
05:26 - What's Next
Solved Recurrence Tree Method
Recursion Tree Method
Recursion tree method | Solving Recurrences | Data Structure & Algorithm | Gate Applied Course
L-2.9: Recurrence Relation [T(n)= 2T(n/2) +cn] | Recursive Tree method | Algorithm
Recurrence Relation T(n)= 2T(n/2) +n | Recursive Tree Method | GATECSE | DAA
Recurrence Relations: Recursion Tree Method
Recurrence Relation T(n)= T(n/3) + T(2n/3) + cn | Recursive Tree Method | GATECSE | DAA
2.1.1 Recurrence Relation (T(n)= T(n-1) + 1) #1
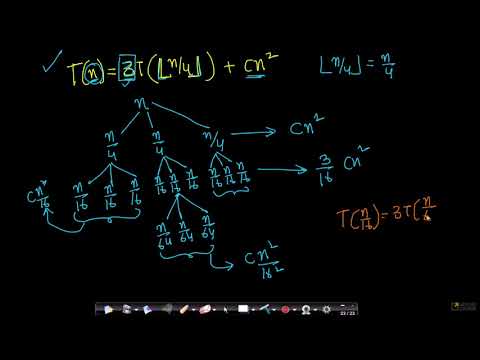
Recurrence Relation T(n)= 3T(n/4) +n^2 | Recursive Tree Method | GATECSE | DAA
L-2.10: Recurrence Relation [T(n)= 3T(n/4) +cn^2] | Recursive Tree method | Algorithm
DAA Session 5: Recursion Tree Method to find time complexity of recursive functions
Introduction to recursion trees
Recursion tree 🔥
Recursion Tree Method
Solve Recurrence using Recursion Tree Method Example1
Recurrence relation: Recursion Tree method - Examples: Set 2
Lec 3.9: Recursive Tree Method | Example 4 | T(n) = 2T(n-1) + 1 | Recurrence Relation in DAA
Tree Method for solving recurrence relations
Recurrence relation: Recursion Tree method - Examples: Set 4
2.1.2 Recurrence Relation (T(n)= T(n-1) + n) #2
Solving Recurrences Example - Fibonacci (Recursion-Tree Method)
Recurrence Relation T(n)= 5T(n/5) +n | Recursive Tree Method | GATECSE | DAA
Recurrence Relations: Solving With The Recursive Tree Method
Solved Recurrence - Iterative Substitution (Plug-and-chug) Method
Комментарии
 0:06:30
0:06:30
 0:32:41
0:32:41
 0:14:15
0:14:15
 0:07:14
0:07:14
 0:07:07
0:07:07
 0:05:40
0:05:40
 0:09:22
0:09:22
 0:13:48
0:13:48
 0:11:20
0:11:20
 0:09:31
0:09:31
 0:14:03
0:14:03
 0:13:36
0:13:36
 0:10:34
0:10:34
 0:14:04
0:14:04
 0:09:53
0:09:53
 0:08:18
0:08:18
 0:08:49
0:08:49
 0:13:45
0:13:45
 0:08:31
0:08:31
 0:16:00
0:16:00
 0:04:35
0:04:35
 0:07:58
0:07:58
 0:09:06
0:09:06
 0:09:08
0:09:08