filmov
tv
Recursion Tree Method

Показать описание
Recursion tree method for solving recurrences running time example
An algorithm analysis example:
What is the running time of the following code ?
Easy Algorithm Analysis Tutorial:
►Please Subscribe !
►Videos:
►Visit my Website:
►Summation Formulas:
►RESOURCES:
Helpful Books:
Algorithm Analysis Books:
Discrete Mathematics Workbooks:
An algorithm analysis example:
What is the running time of the following code ?
Easy Algorithm Analysis Tutorial:
►Please Subscribe !
►Videos:
►Visit my Website:
►Summation Formulas:
►RESOURCES:
Helpful Books:
Algorithm Analysis Books:
Discrete Mathematics Workbooks:
Solved Recurrence Tree Method
Recursion Tree Method
Recursion tree method | Solving Recurrences | Data Structure & Algorithm | Gate Applied Course
Recursion Tree Method
L-2.9: Recurrence Relation [T(n)= 2T(n/2) +cn] | Recursive Tree method | Algorithm
Recursion tree method: intuition | Merge Sort | Data Structure & Algorithm | Appliedroots
Introduction to recursion trees
Solving Recurrences Example - Fibonacci (Recursion-Tree Method)
10 Tree Recursion || Abdul Bari
Recurrence Relation T(n)= 2T(n/2) +n | Recursive Tree Method | GATECSE | DAA
DAA Session 5B: Recursion tree method Examples | T(n) = 2T(n/2) + C | T(n)=T(n/3)+T(2n/3)+n
Solve Recurrence using Recursion Tree Method Example1
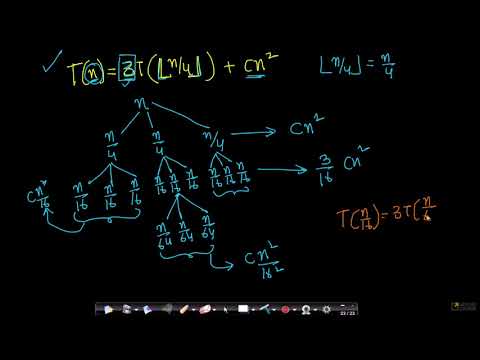
Recurrence Relation T(n)= 3T(n/4) +n^2 | Recursive Tree Method | GATECSE | DAA
Recursion tree 🔥
2.1.1 Recurrence Relation (T(n)= T(n-1) + 1) #1
DAA Session 5: Recursion Tree Method to find time complexity of recursive functions
6.1 - Recursion-Tree Method
Time complexity of Recursive function ( Recursion Tree method )
Recurrence relation: Recursion Tree method - Examples: Set 2
Lec 3.9: Recursive Tree Method | Example 4 | T(n) = 2T(n-1) + 1 | Recurrence Relation in DAA
How Recursion Works? - Explained with animation.
Worked recursion tree example 1
Recursion Tree Method : Example 1 | Solving Recurrences | DAA |
Recurrence Relation T(n)= T(n/3) + T(2n/3) + cn | Recursive Tree Method | GATECSE | DAA
Комментарии
 0:06:30
0:06:30
 0:32:41
0:32:41
 0:14:15
0:14:15
 0:14:04
0:14:04
 0:07:14
0:07:14
 0:12:29
0:12:29
 0:13:36
0:13:36
 0:04:35
0:04:35
 0:17:28
0:17:28
 0:07:07
0:07:07
 0:16:58
0:16:58
 0:09:53
0:09:53
 0:11:20
0:11:20
 0:10:34
0:10:34
 0:13:48
0:13:48
 0:14:03
0:14:03
 0:31:06
0:31:06
 0:07:00
0:07:00
 0:08:18
0:08:18
 0:08:49
0:08:49
 0:03:12
0:03:12
 0:07:19
0:07:19
 0:13:19
0:13:19
 0:09:22
0:09:22