filmov
tv
Implicit derivative of e^(xy^2) = x - y

Показать описание
Implicit derivative of e^(xy^2) = x - y
Derivative of e^xy (Implicit Differentiation) | Calculus 1 Exercises
How do you differentiate e^xy ? ... Use implicit differentiation
find the derivative of e^xy + x^2 - y^2 = 10
using implicit differentiation to find dy/dx for e^(x/y)=x-y
Implicit derivative of e^xy^2 = x y
Partial Derivatives of z =e^(xy)
Derivative of e^(xy)+x²-y²=10 Using Implicit Differentiation | JK Math
Implicit Differentiation
Implicit Differentiation
Implicit Differentiation e ^ x+y = 1 + x^2 y^2
Implicit derivative of e^(xy^2) = x - y
How to Differentiate e^xy #Shorts
Implicit Differentiation with e^y ❖ Calculus 1
FIND dy/dx BY IMPLICIT DIFFERENTIATION | e^(x^2y) = x + y
derivative of x*e^y = x-y (implicit differentiation)
Implicit Differentiation of xy +e^y = x^2
Implicit Differentiation e^x/y=x-y
Find the derivative of x^3 - xy + y^2 = 7 using implicit differentiation
If xy=e^(x+y), find dy/dx | Implicit functions |Methods of Differentiation
Implicit differentiation of xe^y=x-y
STPM/A-level/Pre-U - Implicit differentiation - Part 2
Find dy/dx using implicit differentiation where e^(x/y) = 6x-y.
Trying transition video for the first time 💙😂 || #transformation #transition #shorts #viralvideo...
Комментарии
 0:05:58
0:05:58
 0:03:37
0:03:37
 0:04:13
0:04:13
 0:01:44
0:01:44
 0:03:33
0:03:33
 0:05:58
0:05:58
 0:01:29
0:01:29
 0:11:06
0:11:06
 0:11:45
0:11:45
 0:14:34
0:14:34
 0:04:54
0:04:54
 0:05:58
0:05:58
 0:00:22
0:00:22
 0:03:26
0:03:26
 0:09:04
0:09:04
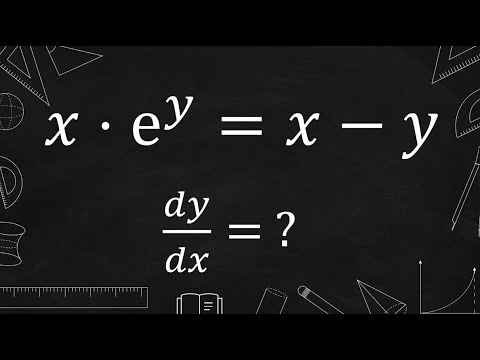 0:02:05
0:02:05
 0:04:20
0:04:20
 0:04:23
0:04:23
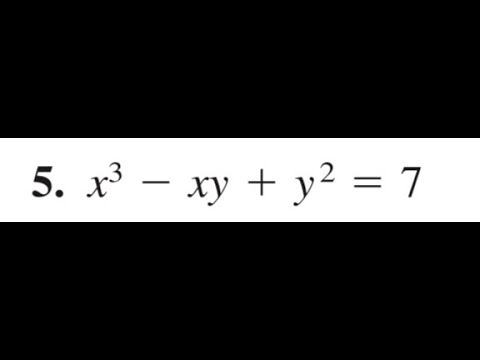 0:01:16
0:01:16
 0:04:57
0:04:57
 0:04:06
0:04:06
 0:07:15
0:07:15
 0:03:44
0:03:44
 0:00:15
0:00:15