filmov
tv
FIND dy/dx BY IMPLICIT DIFFERENTIATION | e^(x^2y) = x + y
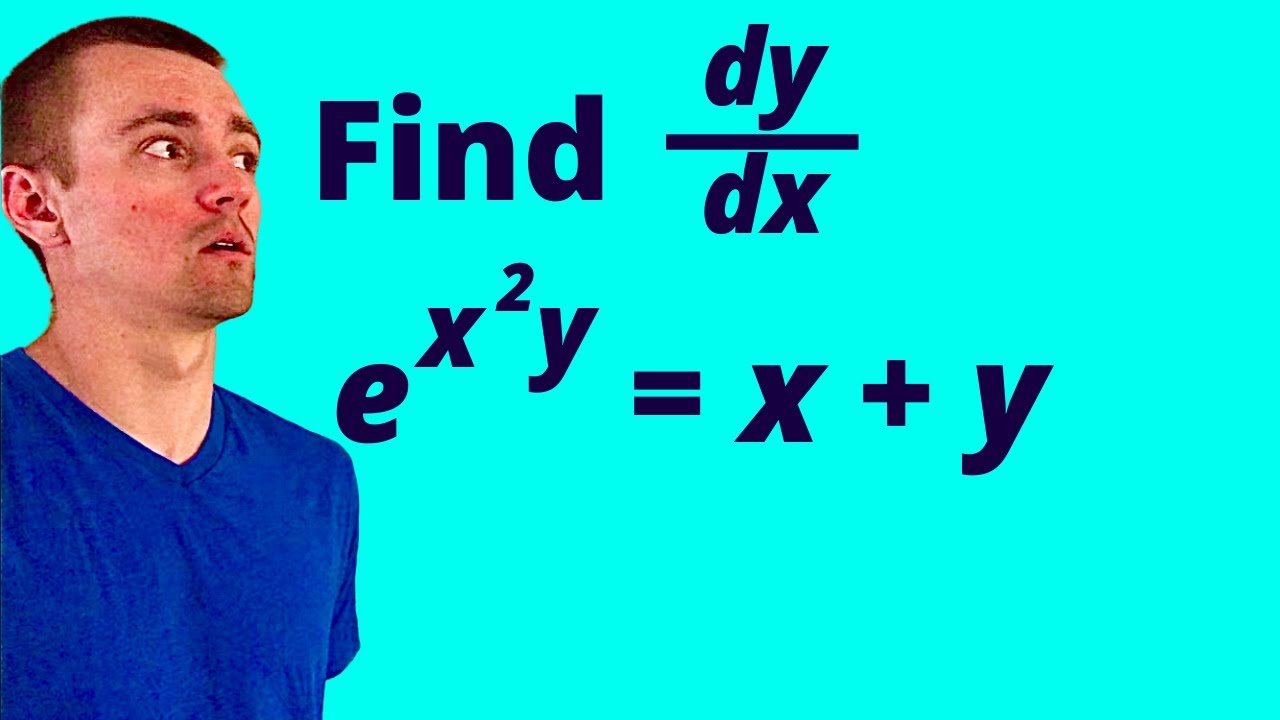
Показать описание
How to find dy/dx by implicit differentiation given that e^(x^2y) = x + y.
Here's the 4 simple steps we will take in order to find dy/dx from the given equation e^(x^2y) = x + y:
0:00 Intro - e^(x^2y) = x + y
0:21 - Take the derivative of both sides with respect to x
3:32 - Separate dy/dx terms from non-dy/dx terms
6:25 - Factor out the dy/dx
7:38 - Isolate dy/dx
READ MORE
WHAT TO WATCH NEXT
YOU MIGHT ALSO BE INTERESTED IN...
Here's the 4 simple steps we will take in order to find dy/dx from the given equation e^(x^2y) = x + y:
0:00 Intro - e^(x^2y) = x + y
0:21 - Take the derivative of both sides with respect to x
3:32 - Separate dy/dx terms from non-dy/dx terms
6:25 - Factor out the dy/dx
7:38 - Isolate dy/dx
READ MORE
WHAT TO WATCH NEXT
YOU MIGHT ALSO BE INTERESTED IN...
Implicit Differentiation
How to use implicit differentiation on an equation for dy dx
How to Do Implicit Differentiation (NancyPi)
Implicit Differentiation
Implicit Differentiation - Find The First & Second Derivatives
Calculus Implicit Differentiation Find dy/dx Example 3
Find dy/dx by implicit differentiation | x^2 - 4xy + y^2 = 4
Calculus 1 Lecture 2.7: Implicit Differentiation
FIND dy/dx BY IMPLICIT DIFFERENTIATION | e^(x^2y) = x + y
❖ Implicit Differentiation for Calculus - More Examples, #1 ❖
Find dy/dx by implicit differentiation. (sinπx +cosπy )^5= 67.
x^2 - y^2 = 1, Find dy/dx by implicit differentiation
Find dy/dx by implicit differentiation | sqrt(x + y) = x^4 + y^4
IMPLICIT DIFFERENTIATION
Find derivative dy/dx of x^2y + xy^2 = 6. Implicit Differentiation
Implicit differentiation with the chain rule and in
Find dy/dx With Implicit Differentiation
Find dy/dx using implicit differentiation where e^(x/y) = 6x-y.
e^(x^2*y) = x + y, Find dy/dx by implicit differentiation
sqrt(x+y) = x Implicit Differentiation find dy/dx
Implicit Differentiation 3x^2 + 2xy + 4y^2 Calculus MCV4U
dy/dx, d/dx, and dy/dt - Derivative Notations in Calculus
Using Implicit Differentiation to Find dy/dx (Example)
How to use implicit differentiation with trig
Комментарии
 0:14:34
0:14:34
 0:03:52
0:03:52
 0:14:17
0:14:17
 0:11:45
0:11:45
 0:12:16
0:12:16
 0:03:26
0:03:26
 0:12:53
0:12:53
 1:08:11
1:08:11
 0:09:04
0:09:04
 0:03:51
0:03:51
 0:04:08
0:04:08
 0:00:35
0:00:35
 0:17:50
0:17:50
 0:10:42
0:10:42
 0:04:05
0:04:05
 0:05:25
0:05:25
 0:03:26
0:03:26
 0:03:44
0:03:44
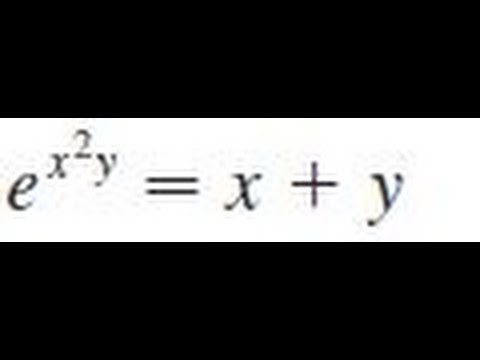 0:02:42
0:02:42
 0:01:51
0:01:51
 0:03:52
0:03:52
 0:06:25
0:06:25
 0:02:45
0:02:45
 0:02:38
0:02:38