Find Max Shear Stress Of Simple Beam with Uniformly Distributed Load Acting on It: Strength of Mat's

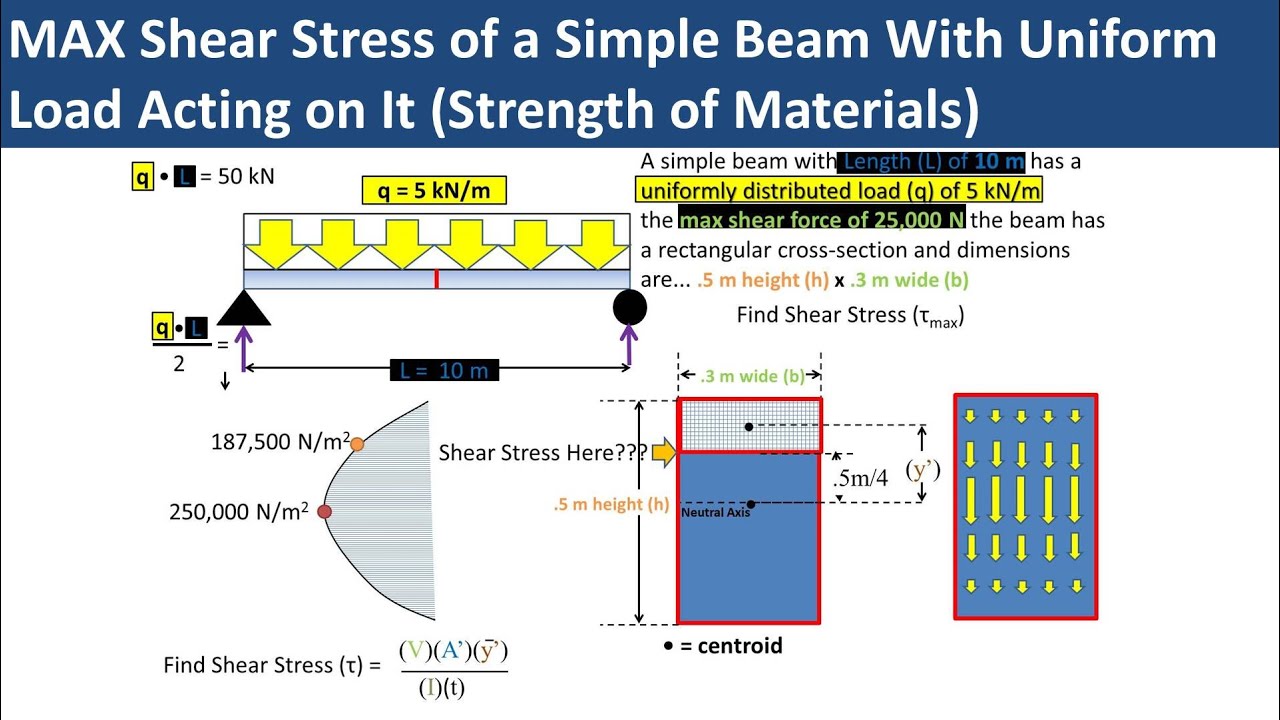
In this problem we have a simple beam with length 10 meters and has a uniformly distributed load q of 5 kilonewtons per meter of beam
In a previous video we found the max shear for this case which was 25 kilo newtons
The beam has a rectangular cross section and the dimension are .5 meters high by .3 meters wide. We want to find the max shear stress on this beam
To complete this problem we will be using the term centroid which is the center of area for a shape which can be found using tables and neutral axis which is a horizontal line that passes through the centroid of the cross section when subjected to pure bending (no axial force)
We will be using the below shear stress equation which I will be going through each variable one by one,
Recall from the previous video where I found the shear diagram for this beam that the max shear force equation is q or disturbed load time the L or total length of the beam over 2. Plugging in our numbers we get 25 kilonewtons.
The A’ is the area below or above the point in question or the area from the point to the outer most fiber. Our point in question will be the neutral axis because this is where max shear stress happens and the area will be the area above the neutral axis which is base times height over 2. Half the cross sectional area
Y bar prime is the distance from the neutral axis to centroid of the area we just found. So in this case it is the height divided by 4.
If you were to be finding the shear stress at another point you would take the area from the desired point up to the outer most edge and find the distance to that centroid from the centroid of the whole cross section.
The plannar moment of inertia can be found by calculs or using a table. In this case which is a rectangle the plannar moment of inertia is the base times the height to the 3rd power over 12.
The final variable is thickness which the rectangle has the same thickness across all points which is the base of .3 meters
Now that we have all of our variables we can plug them in to the equation at the bottom. We get a shear stress max of 250,000 newters per meter squared or pascals
Now if you are like me you want to short cut the process we can reduce the equation for max shear stress to 1.5 time shear force max divided by the area of the cross section. This is only for max shear stress of a rectangle.

Disclaimer
These videos are intended for educational purposes only (students trying to pass a class) If you design or build something based off of these videos you do so at your own risk. I am not a professional engineer and this should not be considered engineering advice. Consult an engineer if you feel you may put someone at risk.