What is Modular Congruence? | Congruence Modulo n, Modular Congruence Definitions

What is modular congruence? What is congruence modulo n? We go over two equivalent definitions of this relation in today’s math lesson! This is your first step to learning modular arithmetic, and can serve as a great gateway to learning about equivalence classes as well! We also briefly discuss modular congruence with negative numbers in the video lesson.

We say that a is congruent to b mod n ( written a ≡ b (mod n) ) if and only if a and b have the same remainders when divided by n. So for example, when we divide 12 by 5, we have a remainder of 2. When we divide 27 by 5, we also have a remainder of 2. Thus, 12 is congruent to 27 mod 5. We can observe the remainders by noticing 12 = 5*2 + 2 and 27 = 5*5 + 2. See? They both have remainder 2!

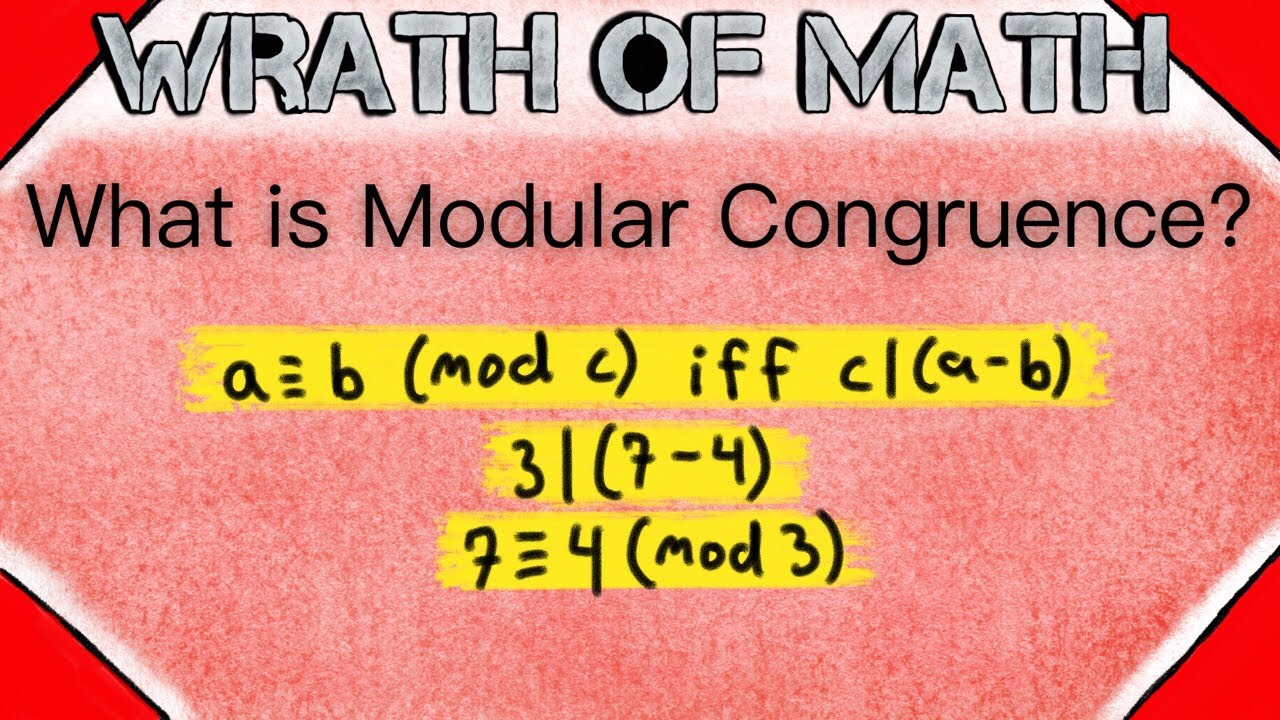
An equivalent definition says that a is congruent to b mod n if and only if n divides a - b, which means that a - b is an integer multiple of n. For example, 20 - 2 = 18, and 6 divides 18. Thus, 20 ≡ 2 (mod 6).

Also, it is important to note that modular congruence is an equivalence relation! Just like “equals”! This means that modular congruence is reflexive, symmetric, and transitive!

I hope you find this video helpful, and be sure to ask any questions down in the comments!

********************************************************************
The outro music is by a favorite musician of mine named Vallow, who, upon my request, kindly gave me permission to use his music in my outros. I usually put my own music in the outros, but I love Vallow's music, and wanted to share it with those of you watching. Please check out all of his wonderful work.

********************************************************************

+WRATH OF MATH+

Follow Wrath of Math on...

[maxien]

I wish i found this before my exams! Absolutely golden explanation

[mandy]

This is the most clear and concise intro to mods I have found on YT. I will definitely be sharing this with my students. Keep up the great instructional content!

[shambo]

Thanks for this clear explanation of how it works for negative numbers. I finally understand it now.

[nancynguyen]

Thank you!! The example right in the beginning helped a lot.

[rajendranchockalingam]

Good morning sir
Excellent explanation
I am from Tamil Nadu
Thank you sir

[luisdfernandez]

On 3:50 do you mean a = 14 and b = 8? Because on the previous example you used the same numbers as an example but got a positive 2 as a remainder and here you get a -2 as remainder.

[johnw]

Thank you! Could you please do a video on solving congruence equation? Ex, ax= b (mod") etc etc. But could you please break it down very easily?

[isfwjey]

Hi, I have doubt. There are 2 ways of solving modulo systems I guess. So my professor gave an example: 14 congruent 2 (mod 12). We solved it like: 14-2=12, and 12 would be an integral multiple of m.
But when I tried the same problem with your method, I am getting different remainders for both. Why is that?

[ahmedmghabat]

3/n(n^2 -1) ? For every n natural
Actually i had it in my previous exam to answer if its true or false .
Please can you solve it?

[yousufh]

thank you, very useful and it helps alot . .

[luisdfernandez]

I have to laugh. I kept asking myself "how did he get 4 as a remainder??" And then, I remembered we're dealing with whole numbers and that 6 can't go into 4 therefore it is 0 and the remainder is the actual 4. It had me scratching my temple for a minute or two LOL

[AbuBakar-fnd]

how to get 2 remainder after dividing 2 by 4

[julventuba]

Can you give example of this theorem?
if ca and cb is congruent mod n, then a and b congruent modulo n/d where d= gcd (c, n)

[exercisefitnesshealth]

thank you for the video, sir.
how about this?
Find x:

1. 8 = x (mod 3)
2. x = 38 (mod 4)

[srinidhinagendran]

I want to know about thereom on this topic

[dkiem]

wiping my tears....still trying to get it

[koshka]

My prof is so garbage compared to these videos
My prof doesn't explain anything, and I'm genuinely trying my hardest to learn
then I go here and you explain it so simply
My tuition should be going here, not my prof