Edmentum Integrated Math1 Unit4 Writing and Solving Systems Using Substitution

Показать описание

*Chapters*
00:00 Tutorial
22:11 Practice
57:30 Mastery Test

A software company is throwing a dinner party for its employees at a hotel. Mr. Spencer recorded the prices for two different catering companies in the table below.

Company Initial Payment Rate Per Employee
Fantastic Catering $135 $12
Devoted Catering $0 $15

Create a system of linear equations that describes the total cost, y, to cater a dinner party for x employees. Write the slope-intercept form of the equation for Fantastic Catering followed by the slope-intercept form of the equation for Devoted Catering. Do not include dollar signs in the equations.

An airport has two long-term parking lots. The cost to park, y, in each lot for x days is shown in the tables.

Lot A
Days Parked Cost
1 $16
2 $20
3 $24
4 $28
Lot B
Days Parked Cost
1 $6
2 $12
3 $18
4 $24

A system of linear equations can be used to determine on which day the cost to park is the same for both lots. One of the equations in the system is y = 6x. What is the other equation in the system?

Nora and Lila are reading the same novel for book club. Nora is on page 128 and plans to read 8 pages per day until the next club meeting. Lila is on page 100 and plans to read 12 pages per day until the next club meeting.

After how many days of reading will Nora and Lila be on the same page of the book? What page will they be on?

A company manufactures two types of cabinets, type 1 and type 2. It produces 110 total cabinets each week.

Last week, the number of type 2 cabinets produced exceeded twice the number of type 1 cabinets produced by 20. If x is the number of type 1 cabinets produced and y is the number of type 2 cabinets produced, the system of equations that represents this situation is x + y = 110 and y = 2x + 20.

What is the solution to this system of equations?
x = 12 − y
2x + 3y = 29
x = 8, y = 4
x = 6, y = 6
x = 7, y = 5
x = 9, y = 3

Jon and Kristen are both increasing the number of minutes they jog each day, as shown in the tables.

Jon
Day Minutes
0 15
1 17
2 19
3 21
Kristen
Day Minutes
0 22
1 23
2 24
3 25

Which system of linear equations could be used to determine which day they will jog for the same number of minutes, where d represents the day and m represents the number of minutes?

m = 15d + 1
m = 22d + 2
m = d + 15
m = 2d + 22
m = 2d + 15
m = d + 22
m = 15d + 2
m = 22d + 1

Joanie runs the concession stand for the school's baseball games. At each game, the best selling items are pretzels and hot dogs. Pretzels are $3 each, and hot dogs are $2 each. Today she sold 15 more hot dogs than pretzels and made $195 in total sales.

Use a system of equations to model the situation above, and determine which of the following are possible amounts of pretzels and hot dogs that Joanie sold today.

35 pretzels, 45 hot dogs
15 pretzels, 30 hot dogs
33 pretzels, 48 hot dogs
31 pretzels, 51 hot dogs

Heather spent a total of 70 minutes working out at the gym. She spent 20 minutes longer running on the treadmill than she spent lifting weights.

When t represents the time Heather spent running on the treadmill and w represents the time she spent lifting weights, which system of equations represents this situation?

What is the solution of the system x − 3y = –13 and 5x + 7y = 34?

`x = (6)/(5)`, y = 4
x = (7)/(2), y = (9)/(2)`
`x = (1)/(2), y = (9)/(2)`
x = –3, y = 7

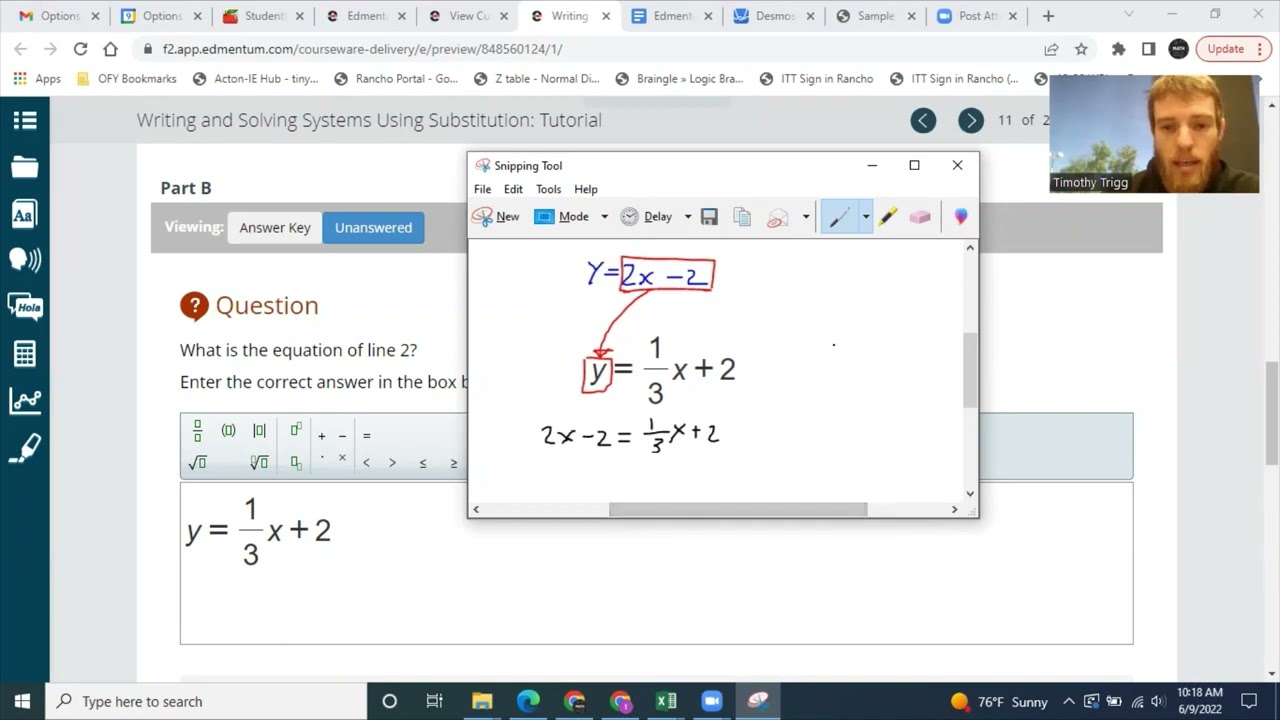
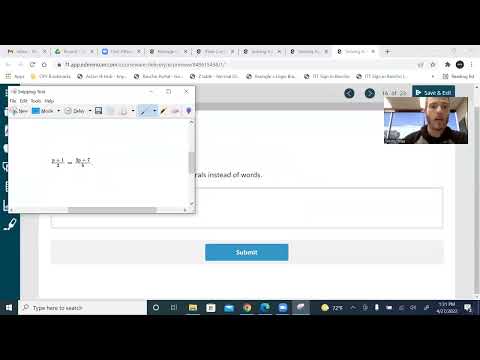
To solve this system of equations using substitution, what could be substituted in place of y in the first equation?

4x = 5 − 2y
y − 2x = 7

The difference of two numbers is 8. When twice the first number is added to three times the second number, the result is 51. What are the two numbers?

12 and 4
15 and 7
20 and 12
23 and 15

Carli and Angela share a cell phone plan and split the bill each month. Last month, their total bill was $109. Carli went over her data limit on her phone, so her share of the bill was $15 more than Angela's to account for the overage charge. Which system of equations represents this situation?