filmov
tv
Matrix Inverse by Gaussian Elimination | Linear Algebra #10

Показать описание
📚About
To compute the inverse, attach the n columns of the identity matrix to form an augmented matrix. By performing elementary row operations on the entire augmented matrix, reduce the coefficient matrix portion to upper-triangular form. Perform back substitution once for every attached column that was produced from the identity matrix. The solution obtained from the original right-hand side [1 0 .. 0] is the first column of the inverse. Continue in the same fashion to obtain columns 2 − n of the inverse.
This lecture is outlined as follows:
00:00 Intro
01:02 Key Representation
02:01 How it works
05:39 Example 1: Invertible Matrix
10:37 Example 2: Non-invertible Matrix
12:44 Summary
In linear algebra, the inverse of a square matrix is another matrix that, when multiplied by the original matrix, results in the identity matrix. The inverse of a matrix A is denoted by A⁻¹, and it exists only for square matrices that are invertible, meaning their determinant is nonzero. The inverse of a matrix is useful for solving systems of linear equations, as well as for finding solutions to many other types of problems in mathematics and science. To find the inverse of a matrix, you can use the following formula:
A⁻¹ = (1/det(A)) * adj(A)
Where det(A) is the determinant of A, adj(A) is the adjugate of A, and * represents matrix multiplication. The adjugate of a matrix A is the transpose of its cofactor matrix. The cofactor matrix is obtained by taking the determinant of every minor of A, and multiplying each of them by the appropriate sign, depending on the position of the element in the matrix.
It is important to note that not all matrices have inverses. A matrix is invertible if and only if its determinant is nonzero. In addition, some matrices have right inverses or left inverses, but not both. A right inverse of a matrix A is a matrix B such that AB = I, where I is the identity matrix. Similarly, a left inverse of A is a matrix B such that BA = I. If a matrix has a right (or left) inverse, it is said to have full column rank (or full row rank).
In summary, the inverse of a matrix is a powerful tool in linear algebra that is used for solving systems of linear equations and many other types of problems. It exists only for square matrices that are invertible, and is computed using a formula that involves the determinant, adjugate, and cofactor matrix of the original matrix.
●▬▬▬▬▬▬▬๑۩۩๑▬▬▬▬▬▬▬▬●
_*****╔═╦╗╔╦╗╔═╦═╦╦╦╦╗╔═╗***** _
_*****║╚╣║║║╚╣╚╣╔╣╔╣║╚╣═╣***** _
_*****╠╗║╚╝║║╠╗║╚╣║║║║║═╣***** _
_*****╚═╩══╩═╩═╩═╩╝╚╩═╩═╝***** _
●▬▬▬▬▬▬▬๑۩۩๑▬▬▬▬▬▬▬▬●
Комментарии
 0:13:13
0:13:13
 0:05:09
0:05:09
 0:07:43
0:07:43
 0:15:21
0:15:21
 0:05:59
0:05:59
 0:18:40
0:18:40
 0:11:44
0:11:44
 0:14:03
0:14:03
 0:13:37
0:13:37
 0:08:04
0:08:04
 0:15:51
0:15:51
 0:03:15
0:03:15
 0:08:24
0:08:24
 0:05:32
0:05:32
 0:04:59
0:04:59
 0:10:51
0:10:51
 0:08:04
0:08:04
 0:19:34
0:19:34
 0:12:09
0:12:09
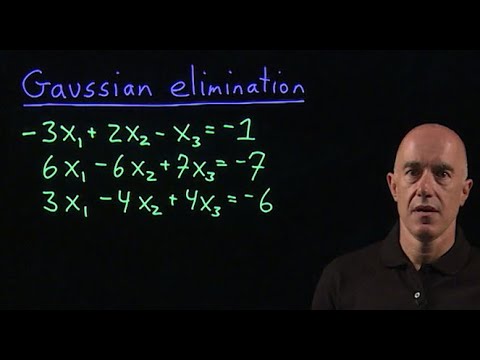 0:14:00
0:14:00
 0:09:08
0:09:08
 0:11:22
0:11:22
 0:18:04
0:18:04
 0:15:48
0:15:48