filmov
tv
Related Rates | Gravel Cone Pile Height

Показать описание
In this video, we use related rates to determine the rate of change of the heigh of a gravel cone pile.
#calculus #relatedrates
#calculus #relatedrates
Related Rates - Gravel Dumped Into Conical Tank Problem
Related Rates 4: Gravel expanding a Cone
Calculus Related Rates: Volume of a Cone (Sand/Gravel Conical Pile)
Related Rates: Volume of a Cone: Gravel from a Conveyor Belt
Related Rates | Gravel Cone Pile Height
Related rates: water pouring into a cone | AP Calculus AB | Khan Academy
Related Rates Cone Example (Calculus)
Ex: Related Rates - Right Circular Cone
Related Rates Cone Problem
AP Calculus 3-5C Related Rates Gravel Pile Problem
The Related Rates Gravel Problem (Calculus Shorts)
Step by Step Method of Solving Related Rates Problems - Conical Example
MathCamp321: Calculus - Related Rates Cones
Related Rates Applicate: Leaking Conical Tank
Hard Calculus Problems Made EASY!! (Related Rates)
Gravel is being dumped from a conveyor belt at a rate of 30 ft3/min, and its coarseness is such that
MathCamp321: Calculus: Related Rates (Cone)
Calculus Related Rates - How Fast is a Conical Sand Pile Changing
Related Rates: Find the Rate of Change in the Water Height as it Drains from a Right Circular Cone
How to Solve Related Rates Problems - PART 1 #calculus #apcalculus #math #mathtrick #mathstricks
Related Rates #2 Using Cones
Related Rate Cone Problem
The Volume of a Cone Problem - Related Rates
Related Rates Cone Problem (with proportions)
Комментарии
 0:14:57
0:14:57
 0:04:59
0:04:59
 0:02:51
0:02:51
 0:08:05
0:08:05
 0:01:00
0:01:00
 0:11:32
0:11:32
 0:05:31
0:05:31
 0:06:54
0:06:54
 0:07:34
0:07:34
 0:09:56
0:09:56
 0:02:18
0:02:18
 0:09:42
0:09:42
 0:07:22
0:07:22
 0:07:13
0:07:13
 0:00:59
0:00:59
 0:05:11
0:05:11
 0:05:17
0:05:17
 0:06:47
0:06:47
 0:05:05
0:05:05
 0:00:39
0:00:39
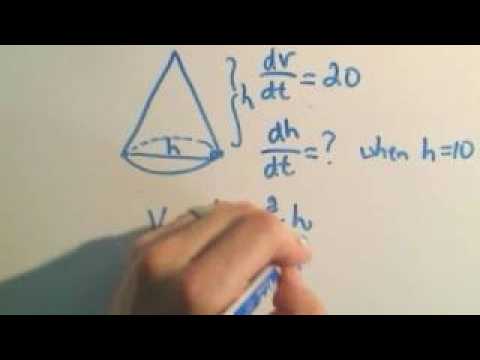 0:02:47
0:02:47
 0:13:35
0:13:35
 0:08:42
0:08:42
 0:07:20
0:07:20