filmov
tv
Cofactor expansion
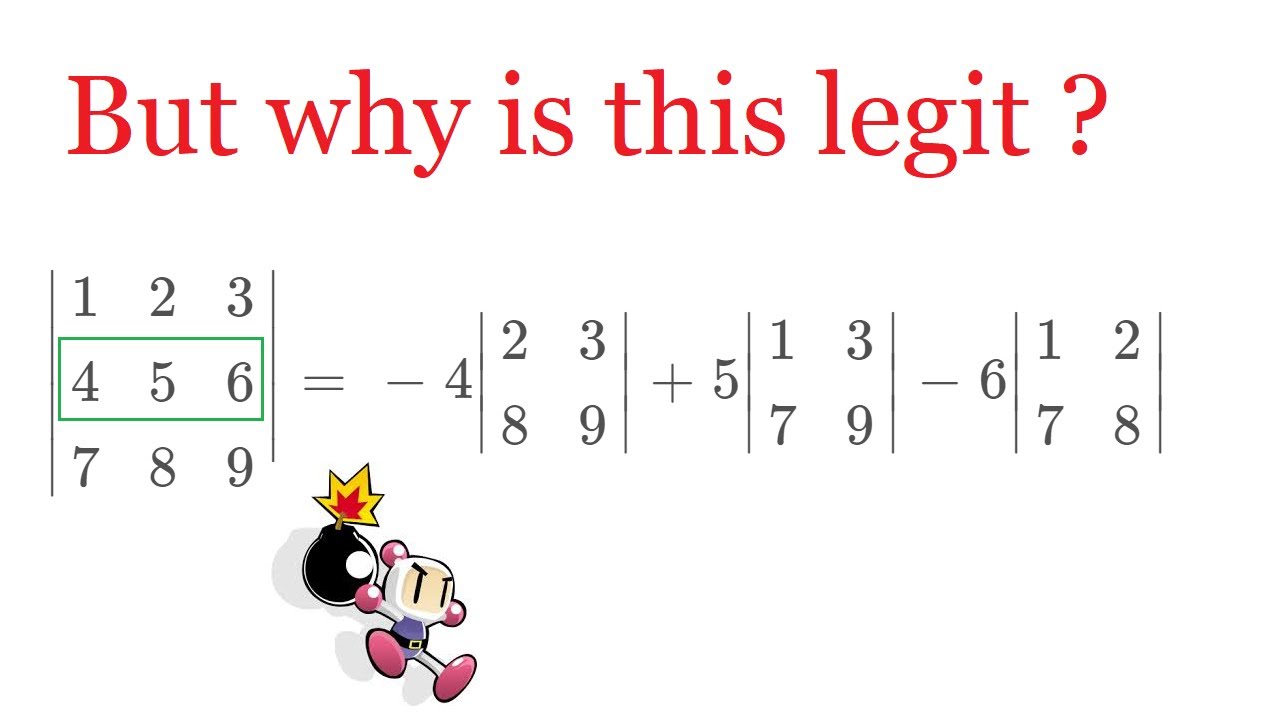
Показать описание
Cofactor expansion along any row
Have you ever wondered why you can expand the determinant along any row and still get the same answer? In this video, I show why it's true! Enjoy
Have you ever wondered why you can expand the determinant along any row and still get the same answer? In this video, I show why it's true! Enjoy
The Determinant of a 4 by 4 Matrix Using Cofactor Expansion (Expansion by Minors)
[Linear Algebra] Cofactor Expansion
Find the determinant of a 3x3 matrix using cofactor expansion
How do you use Cofactor Expansion to find the Determinant of a 4x4 Matrix?
Finding a determinant using cofactor expansion
Linear Algebra: Ch 2 - Determinants (22 of 48) The Cofactor of a Matrix
Cofactor expansion
Example 2: Finding the determinant of a matrix using cofactor expansion
Finding Determinants Using Cofactor Expansion Method (Tagalog/Filipino Math)
The Cofactor Definition of Determinants (Laplace Expansion Explained) | Linear Algebra
a3 1 4 Cofactor expansion
Linear Algebra 2.1 Determinants by Cofactor Expansion
Linear Algebra 3.1.2 Co-factor Expansion
Linear Algebra: Find the Determinant of a Square Matrix Using Cofactor Expansion
Cofactor Expansion
Theorem 2.1.1 (Cofactor Expansion Theorem)
Cofactor Expansion Proof
2.1 - Determinants by Cofactors Expansion
Cofactor Expansion
How To Find The Determinant of a 4x4 Matrix
2.1 Determinants by Cofactor Expansion
Math 240 - Chapter 3 - Determinants using Cofactor Expansion - The Plug and Chug Series #6
MATHS211 sec2.1: determinants by cofactor expansion
Determinant of a matrix using cofactor expansion
Комментарии
 0:06:33
0:06:33
![[Linear Algebra] Cofactor](https://i.ytimg.com/vi/ZAECu1mkFY8/hqdefault.jpg) 0:12:12
0:12:12
 0:07:26
0:07:26
 0:03:29
0:03:29
 0:07:58
0:07:58
 0:04:13
0:04:13
 0:31:12
0:31:12
 0:06:29
0:06:29
 0:25:34
0:25:34
 0:14:29
0:14:29
 0:09:36
0:09:36
 0:22:50
0:22:50
 0:16:18
0:16:18
 0:08:34
0:08:34
 0:09:39
0:09:39
 0:17:36
0:17:36
 0:04:38
0:04:38
 0:20:26
0:20:26
 0:01:41
0:01:41
 0:11:29
0:11:29
 0:05:54
0:05:54
 0:12:32
0:12:32
 0:19:31
0:19:31
 0:01:22
0:01:22