filmov
tv
Ramanujan wins again!!

Показать описание
Ramanujan would be proud!!
We calculate the integral from 0 to infinity of sin x^n using Ramanujan's master theorem. This involves by writing the function out as a Taylor or Maclaurin series and then converting it into the Gamma function, which is a generalization of the factorial function. We also use Euler's formula which relates the gamma function with sin and cos. This is a must see for anyone who appreciates Srinivasa Ramanujan's work and math and calculus in general
We calculate the integral from 0 to infinity of sin x^n using Ramanujan's master theorem. This involves by writing the function out as a Taylor or Maclaurin series and then converting it into the Gamma function, which is a generalization of the factorial function. We also use Euler's formula which relates the gamma function with sin and cos. This is a must see for anyone who appreciates Srinivasa Ramanujan's work and math and calculus in general
Ramanujan wins again!!
Leave It To Ramanujan
Last Words of Albert Einstein #shorts
Ramanujan Learned Math With This Book
Bill Gates Vs Human Calculator
Why Ravan didn’t r*pe Sita? | Keerthi History #india #shorts #ramayan...
THIS WAS UNEXPECTED😱😲 | Social Awareness Video By 3rd Eye | #Shorts |#YoutubeShorts
Only for a Genius! Connect 1 to 1, 2 to 2 & 3 to 3 without crossing the lines! #math #youtube
This CIA guy right about India🇮🇳🤷♂️ #shorts #cia
India vs japan || mathematics challenge || 😅🤣🤣🤭
How Karma is paying back to the Britain | Keerthi History #india #shorts
Stephen Hawking's Famous Speech.
John Cena as a Referee | John Cena Help Randy Orton to Win The Match #shorts
Abhinay Vaddi In Ramanujan
America🇺🇸 Vs. India🇮🇳 AT ATM😂 Relatable? #shorts #imkavy
Pakistani Man's Hilarious Reaction On Chandrayaan 3 Goes Viral | Pakistan Reaction On Chandraya...
RAMANUJAN YATRA -- Prof M Ram Murty
BOARD MARK'S DOESN'T MATTER 🔥💯 | #viral #motivation #failure #shorts #iit #upsc #ias #iasm...
The Evolution of The Undertaker: From Childhood to Wrestling Icon | WWE Journey
Naruto entering god mode
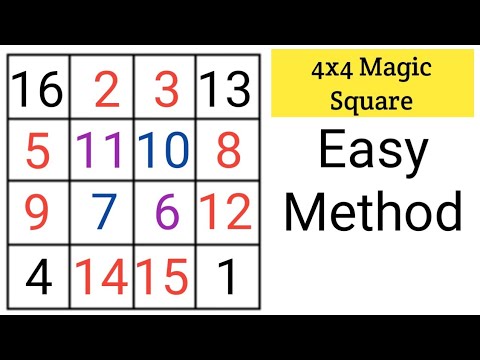
4x4 magic square | 4 by 4 magic Square | magic square | magic square 4x4 | Maths magic tricks
BRAUN STROWMAN'S POWER💪👿 || #shorts #youtubeshorts #braunstrowman #wwe
where is Albert Einstein brain ?
Teammate's Mic 😭😑
Комментарии
 0:09:13
0:09:13
 0:00:11
0:00:11
 0:00:37
0:00:37
 0:09:32
0:09:32
 0:00:51
0:00:51
 0:00:57
0:00:57
 0:00:41
0:00:41
 0:00:20
0:00:20
 0:00:51
0:00:51
 0:00:12
0:00:12
 0:00:17
0:00:17
 0:00:47
0:00:47
 0:00:22
0:00:22
 0:01:15
0:01:15
 0:00:29
0:00:29
 0:00:17
0:00:17
 1:23:06
1:23:06
 0:00:22
0:00:22
 0:00:20
0:00:20
 0:00:35
0:00:35
 0:01:59
0:01:59
 0:00:16
0:00:16
 0:00:34
0:00:34
 0:00:13
0:00:13