Calculus 1, Lec 26A: Maximize the Viewing Angle for a Statue, Mathematica Animations, Logistic Model

To get the best view of a statue, how far from the base should you stand to maximize the viewing angle?

(0:00) Lecture plan.
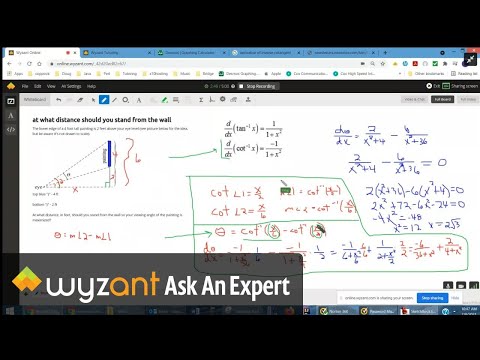
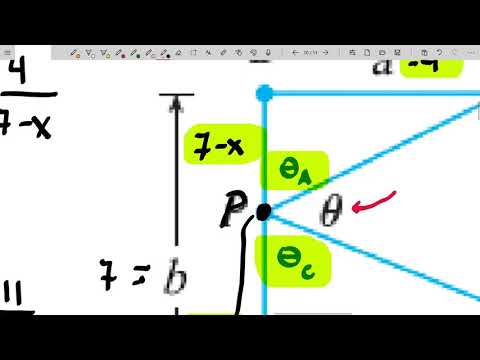
(0:43) Maximize the viewing angle for a statute (like the Statue of Liberty). The function to maximize is the difference of two inverse tangent functions (arctangent functions).
(7:26) Show the derivation of the critical point in terms of two parameters H (the height of the statue) and P (the height of the pedestal) on a powerpoint slide.
(13:24) Use Mathematica to input the function and ultimately make an interactive graph showing the maximum point. The second derivative is not always negative, but it is negative at the critical point, so the Second Derivative Test can be used to say the point is a local maximum.
(20:36) Use Graphics and Line in Mathematica to make an animated picture of the situation, allowing for x, P, and H to change with a slider.
(27:55) Logistic differential equation model (review and symbolically check that the function derived with DSolveValue in Mathematica is a solution).

The Statue of Liberty is 92 meters high, including the 46 meter pedestal upon which it stands. How far from the base should an individual stand to ensure that the view angle, theta, is maximized?

[natewestberg]

When he asked what was my least favorite math subject, I instinctively said calculus...lol!