filmov
tv
The convolution theorem and polynomial multiplication

Показать описание
This revision fixes the following errors and suggestions that were found by my readers:
This update continues the journey of understanding transfer functions. It provides a brief understanding of the difference between the time domain and the frequency domain. I hint at the awesomeness that is the Fourier Transform (more to come on this!) and show how convolution in the time domain is really just multiplication in the frequency domain.
There is also a new side note in the convolution section - as was recommended by a reader - that shows how polynomial multiplication is really just discrete convolution of the polynomial coefficients. Pretty cool actually.
Thank you for all of your support and I hope this helps you on your quest to understand control theory on a more intuitive level. Cheers!
The convolution theorem and polynomial multiplication
But what is a convolution?
Video5-18: Convolution Theorem, proof, examples, application. Elementary differential equations
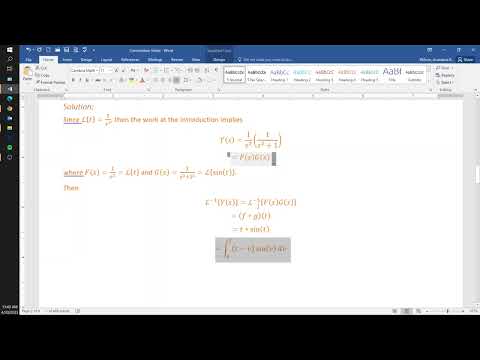
inverse laplace of s/(s^2+1)^2, using convolution theorem
Video5-17: Convolution Theorem, examples of convolution. Elementary differential equations
Convolution Part 4
7.4 Example - Application of Convolution Theorem
Convolution Theorem for y'-2y=e^t, y(0)=0
Quiz 5 Problem 1 Convolution of a Polynomial with Sine
Convolution of f(t)=g(t)=e^(at)
Laplace Transform of the Convolution of t^2 and te^t
Convolution Intuition
Convolution Theorem (with proof)
Convolution Integral Example 02 - Convolution of Two Polynomials
Convolution Theorem
Finding an Inverse Transform by Convolution Theorem
Convolution Theorem: f(t) = t^2 ; g(t) = t^3 ; Find (f*g)(t)
3.4 The Convolution Theorem
Convolution theorem
Convolution Theorem / Laplace transform / MMP
AU MATH 3020 Dr Wilson Convolution 2 Convolution Theorem Example
Convolution Theorem
Find Inverse Laplace Transform using Convolution Theorem of s^2/(s^2+4)^2
Inverse Laplace using Convolution theorem
Комментарии
 0:07:55
0:07:55
 0:23:01
0:23:01
 0:22:22
0:22:22
 0:09:25
0:09:25
 0:19:56
0:19:56
 0:15:09
0:15:09
 0:04:41
0:04:41
 0:04:24
0:04:24
 0:06:48
0:06:48
 0:00:53
0:00:53
 0:03:03
0:03:03
 0:07:52
0:07:52
 0:18:30
0:18:30
 0:14:14
0:14:14
 0:07:42
0:07:42
 0:02:32
0:02:32
 0:00:45
0:00:45
 0:25:27
0:25:27
 0:03:31
0:03:31
 0:20:32
0:20:32
 0:05:12
0:05:12
 0:14:00
0:14:00
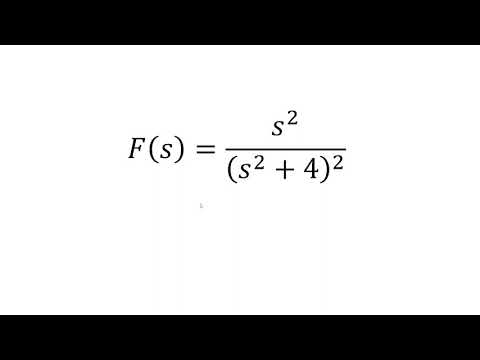 0:02:32
0:02:32
 0:07:05
0:07:05