filmov
tv
Gaussian Integral 6 Gamma Function

Показать описание
Welcome to the awesome 12-part series on the Gaussian integral. In this series of videos, I calculate the Gaussian integral in 12 different ways. Which method is the best? Watch and find out!
In this video, I calculate the Gaussian integral by using properties of the gamma function, which is a real-variable analog of the factorial function.
In this video, I calculate the Gaussian integral by using properties of the gamma function, which is a real-variable analog of the factorial function.
Gaussian Integral 6 Gamma Function
Gaussian Integral Using Gamma Function
Calculating Gamma 1/2 using Gaussian Integration
Solving the Gaussian integral using the Gamma function
Gaussian Integral By Beta and Gamma functions
Gaussian integral, Gamma function and Hypersphere | Short derivation of math results
The Gaussian Integral using Gamma function | CT Academy | Maths for Fun | Numberphile | Pawan Shukla
Solving the Gaussian Integral
Gamma Function and Gaussian Integrals
Some Gaussian integrals and their wave forms l Integration
Solving the Gaussian Integral using Power Series
Integration using gamma function for gaussian distribution function
Lemma: A Generalised Gaussian in terms of the Gamma function.
Dr. Zufelt explains how to evaluate the Gaussian Integral
The Super Gaussian Integral (The Art of Integration)
Introducing Gama Function (Also Destroying Gaussian Integral)
How REAL Men Integrate Functions
These complex gaussian integrals are awesome!
When mathematicians get bored (ep1)
This chapter closes now, for the next one to begin. 🥂✨.#iitbombay #convocation
Math Integration Timelapse | Real-life Application of Calculus #math #maths #justicethetutor
The Gaussian Integral
Video#6: Gaussian Integral
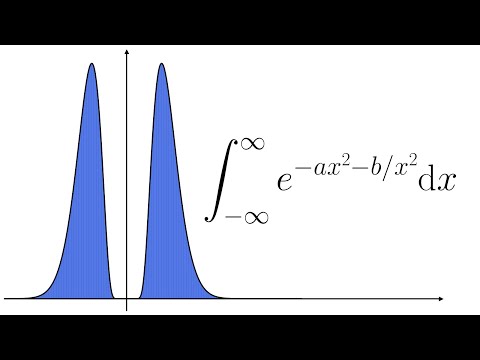
A Gaussian-like integral evaluated using partial differentiation: ∫exp(−ax²−b/x²)dx
Комментарии
 0:08:42
0:08:42
 0:02:00
0:02:00
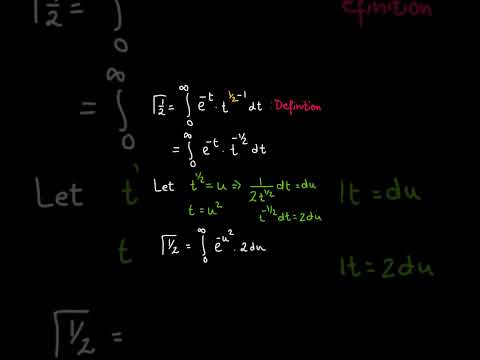 0:00:34
0:00:34
 0:06:19
0:06:19
 0:15:37
0:15:37
 0:06:58
0:06:58
 0:06:15
0:06:15
 0:07:11
0:07:11
 0:42:10
0:42:10
 0:00:12
0:00:12
 0:04:38
0:04:38
 0:03:57
0:03:57
 0:02:59
0:02:59
 0:01:35
0:01:35
 0:07:45
0:07:45
 0:13:36
0:13:36
 0:00:35
0:00:35
 0:11:11
0:11:11
 0:00:37
0:00:37
 0:00:16
0:00:16
 0:00:09
0:00:09
 0:10:09
0:10:09
 0:16:06
0:16:06
 0:12:27
0:12:27