Neural Networks Expressivity through the lens of Dynamical Systems

Title: Neural Networks Expressivity through the lens of Dynamical Systems

Speaker: Vaggos Chatziafratis (UC Santa Cruz)

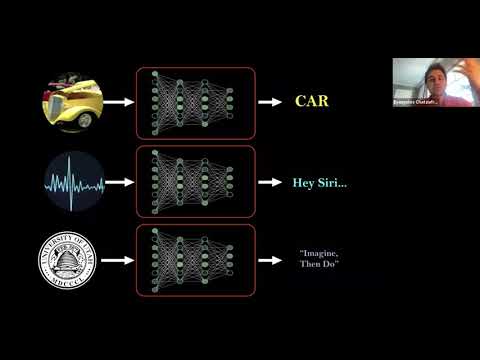
Abstract. Given a target function f, how large must a neural network be in order to approximate f? Understanding the representational power of Deep Neural Networks (DNNs) and how their structural properties (e.g., depth, width, type of activation unit) affect the functions they can compute, has been an important yet challenging question in approximation theory and deep learning even in the early days of AI.

In this talk, I want to tell you about some recent progress on this topic that uses ideas from dynamical systems. The main results are exponential depth-width trade-offs for DNNs representing certain families of functions. Our techniques rely on a generalized notion of fixed points, called periodic points that have played a major role in chaos theory (Li-Yorke chaos and Sharkovsky's theorem).