filmov
tv
p^q=p (mod pq) - Fermat's Medium Sized Theorem

Показать описание
#Shorts
Hi,
In this video I'll be proving a fun result from number theory. We want to prove that p^q is congruent to p (mod pq) where p and q are distinct primes. To prove this we'll be using some fundamental properties of modular arithmetic, as well as Fermat's Little Theorem.
Follow me on Instagram: @jpimaths
And, as always, any comments, feedback or suggestions are welcomed!
Thanks.
Hi,
In this video I'll be proving a fun result from number theory. We want to prove that p^q is congruent to p (mod pq) where p and q are distinct primes. To prove this we'll be using some fundamental properties of modular arithmetic, as well as Fermat's Little Theorem.
Follow me on Instagram: @jpimaths
And, as always, any comments, feedback or suggestions are welcomed!
Thanks.
p^q=p (mod pq) - Fermat's Medium Sized Theorem
Number Theory | Corollaries to Fermat's Little Theorem
003: APPLICATIONS OF FERMAT THEOREM
if p and q are distinct primes,then p^(q-1) + q^(p-1) = 1(mod pq) #hpu #primes
Euler’s phi(pq) for primes p and q
Fermat's Last Theorem: More Properties of Galois Reps Attached to Elliptic Curves! (1.12, 10b)
Fermat and Euler's Theorems: RSA Cryptography
Euler’s Totient Function (Phi Function)
Extended Euclidean Algorithm and Inverse Modulo Tutorial
What does a ≡ b (mod n) mean? Basic Modular Arithmetic, Congruence
Arithmétique dans Z - Petit Théorème de Fermat - 2 Bac SM - [Exercice 37]
FERMAT'S LITTLE THEOREM
Fermat's Last Theorem: Moduli Spaces of Elliptic Curves! (3.5, #28)
Converse of Fermat’s Theorem
CS2050 L17 Fermat's Little Theorem and Euler's Theorem
Symmetric Problem on Divisibility of Primes by @letsthinkcritically
Number Theory-1(Divisibility,The Fermat's Little Theorem,Fermat Theorem)
Journey into Number Theory: Chapter 1:Section 6
Fermat's Last Theorem: The Mysterious Frey Curve! (1.7, 6)
Cryptography #Module 3 1 NCS fermats theorem
Square Root 2 Is Not Rational - Complex Numbers and Elliptic Curves (FLT Proof #4.3.1.1a)
Fermat's Last Theorem: The Weil Pairing! (3.3, #26)
147 - Pequeno Teorema de Fermat e Criptografia
Fermat's Last Theorem: Raynaud's Theorems! (5.21, 87)
Комментарии
 0:00:59
0:00:59
 0:08:32
0:08:32
 0:11:50
0:11:50
 0:05:14
0:05:14
 0:03:41
0:03:41
 0:07:44
0:07:44
 0:20:00
0:20:00
 0:08:40
0:08:40
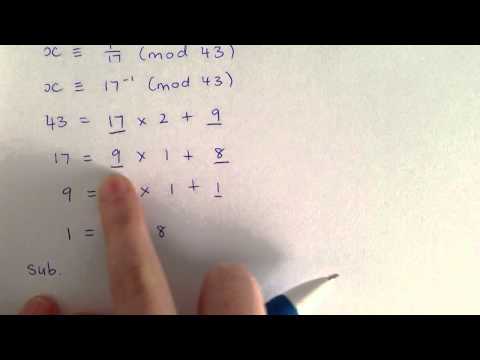 0:06:00
0:06:00
 0:05:45
0:05:45
 0:23:36
0:23:36
 0:33:17
0:33:17
 0:11:16
0:11:16
 0:04:34
0:04:34
 0:57:00
0:57:00
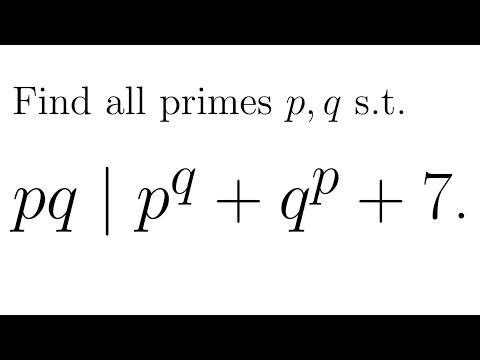 0:09:41
0:09:41
 1:49:01
1:49:01
 0:20:38
0:20:38
 0:13:05
0:13:05
 0:08:40
0:08:40
 0:11:01
0:11:01
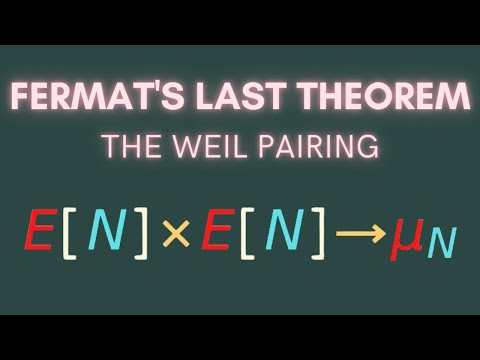 0:10:18
0:10:18
 0:08:12
0:08:12
 0:09:22
0:09:22