filmov
tv
Angle Sum Formulae: Proof using Ptolemy's Theorem
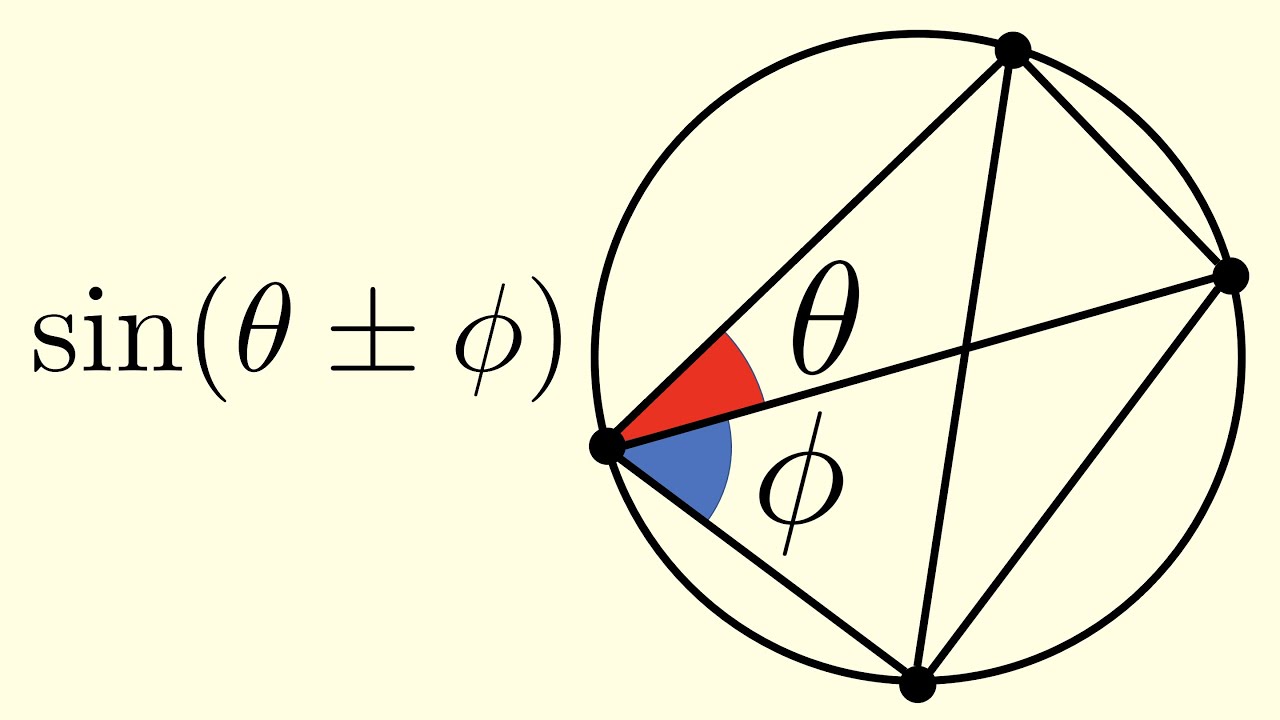
Показать описание
We prove the angle sum and difference identities for sin(θ ± ϕ), using Ptolemy's theorem.
00:00 Setup
00:51 sin(θ + ϕ)
02:24 Finding |BD|
05:56 Lemma
06:25 sin(θ - ϕ)
00:00 Setup
00:51 sin(θ + ϕ)
02:24 Finding |BD|
05:56 Lemma
06:25 sin(θ - ϕ)
Angle Sum Formula Proof with Linear Algebra!
A proof to remember: Double Angle Formulas I (visual proof)
Proof of angle addition formula for sine | Trigonometry | Khan Academy
Trigonometry | Double Angle Formulae - Proof, Worked Examples and Trial Questions
Angle Sum formula, proof by complex number
Proof of the tangent angle sum and difference identities
Proving the Double and Half Angle Formulas for Trigonometry (Precalculus - Trigonometry 27)
A-Level Maths: E6-01 Compound Angles: Proving the Compound Angle Formulae
Angle Between Radius Vector and Tangent | Engineering Mathematics 1
The Double-Angle Formulas | proof without words| mathocube|
TR-38: Angle Sum and Difference Identities (Trigonometry series by Dennis F. Davis)
An Angle Sum Problem (with a visual solution)
Double Angle Formula
Proof: Angle Sum/Difference Trig Identities (TAN)
Proof of angle addition formula for cosine | Trigonometry | Khan Academy
Compound Angle Identities (1 of 3: Proving sin(a+b) geometrically)
Angle Sum Property Activity ! 180 Degree #maths #angles #2023 #triangle #formula #activity #diy
Proof: Angle Sum Trig Identities (SIN and COS)
Double Angle Identities & Formulas of Sin, Cos & Tan - Trigonometry
A proof for sin(a+b) and cos(a+b) that you probably haven’t seen before
Visualizing the Interior Angle Sum Of A Triangle | Geometric Relationships
Verifying Trigonometric Identities With Double Angle Formulas
ANGLE THEOREMS - Top 10 Must Know
Proof of the Angle Sum Formulas
Комментарии
 0:01:59
0:01:59
 0:02:01
0:02:01
 0:08:26
0:08:26
 0:19:21
0:19:21
 0:05:02
0:05:02
 0:06:55
0:06:55
 0:27:17
0:27:17
 0:14:39
0:14:39
 0:15:42
0:15:42
 0:02:36
0:02:36
 0:07:54
0:07:54
 0:02:33
0:02:33
 0:00:54
0:00:54
 0:04:02
0:04:02
 0:06:02
0:06:02
 0:13:19
0:13:19
 0:00:31
0:00:31
 0:03:46
0:03:46
 0:18:16
0:18:16
 0:06:29
0:06:29
 0:00:15
0:00:15
 0:15:19
0:15:19
 0:20:47
0:20:47
 0:04:36
0:04:36