filmov
tv
Multiplying 41*37 with Fast Fourier Transform by hand

Показать описание
For large numbers, the elementary method of multiplication (convolution method) is FAR too slow.
Instead, using the rule that time domain convolution is equivalent to frequency domain point-wise multiplication, by travelling to the frequency domain and using point-wise multiplication, we can utilize the Fast Fourier Transform which removes redundant aliasing calculations.
1. The extra zeros to begin allow for tens column to overflow once multiplication occurs. More generally, tacking on zeros prior to convolution is known as zero-padding for a linear convolution. Without zeros, calculations will overflow into the next period and has a name as well: circular convolution.
2. I keep saying half cycle/second twiddle factor. Technically, its half cycle vs unit frequency period but you can intuitively imagine twiddle factor tracing the unit circle over a unit 1 sec time frame so I say that...
3. Half cycle/unit frequency period twiddle factor condenses because of conjugate symmetry of powers of 2. If not radix 2 transform, no symmetry exists and the twiddle factor generalizes to 1 cycle/unit frequency period where the frequency period first is periodically extended to the size of the upsample.
This video passes over intricacies of the FFT. You may find hefty tutorials at my Facebook Tutorial Website:
Math Music Tutorials (mrpolygon37)
Instead, using the rule that time domain convolution is equivalent to frequency domain point-wise multiplication, by travelling to the frequency domain and using point-wise multiplication, we can utilize the Fast Fourier Transform which removes redundant aliasing calculations.
1. The extra zeros to begin allow for tens column to overflow once multiplication occurs. More generally, tacking on zeros prior to convolution is known as zero-padding for a linear convolution. Without zeros, calculations will overflow into the next period and has a name as well: circular convolution.
2. I keep saying half cycle/second twiddle factor. Technically, its half cycle vs unit frequency period but you can intuitively imagine twiddle factor tracing the unit circle over a unit 1 sec time frame so I say that...
3. Half cycle/unit frequency period twiddle factor condenses because of conjugate symmetry of powers of 2. If not radix 2 transform, no symmetry exists and the twiddle factor generalizes to 1 cycle/unit frequency period where the frequency period first is periodically extended to the size of the upsample.
This video passes over intricacies of the FFT. You may find hefty tutorials at my Facebook Tutorial Website:
Math Music Tutorials (mrpolygon37)
Комментарии
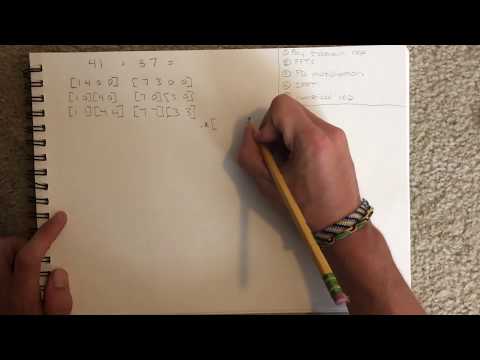 0:07:01
0:07:01
 0:13:58
0:13:58
 0:04:40
0:04:40
 0:01:04
0:01:04
 0:00:57
0:00:57
 0:00:14
0:00:14
 0:07:25
0:07:25
 0:12:00
0:12:00
 1:06:23
1:06:23
 0:09:21
0:09:21
 0:11:01
0:11:01
 0:03:47
0:03:47
 0:24:15
0:24:15
 0:21:01
0:21:01
 0:20:35
0:20:35
 0:04:53
0:04:53
 0:01:41
0:01:41
 0:00:29
0:00:29
 0:26:04
0:26:04
 0:12:13
0:12:13
 0:02:29
0:02:29
 0:09:31
0:09:31
 0:11:02
0:11:02
 0:14:56
0:14:56