filmov
tv
This is one of the coolest integrals ever solved
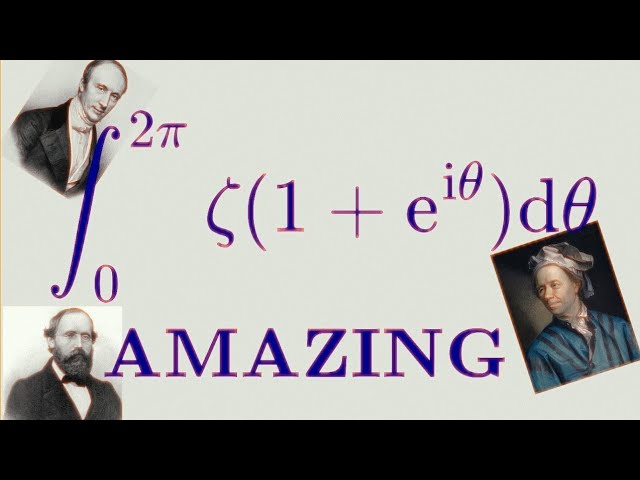
Показать описание
My complex analysis lectures:
Support my work and get early access to content via Patreon:
You can follow me on Instagram for write ups that come in handy for my videos and DM me in case you need math help:
My LinkedIn:
Advanced MathWear:
Support my work and get early access to content via Patreon:
You can follow me on Instagram for write ups that come in handy for my videos and DM me in case you need math help:
My LinkedIn:
Advanced MathWear:
I Meet MrBeast To Break The Internet!!
This Is One Of Those Moments
National security analyst: This is one of the scariest things I've said on TV
This is one of the greatest scenes ever.
This is one of the BIGGEST lies in PC Building...
This is one of the weirdest reactions I've ever seen
This Is One of the Most Inspiring Things I’ve Ever Seen
This is one of the funniest things I've ever seen
This Is One of the Smallest Restaurants in New York
This is one of the RAREST Tesla Collectables 😳👀
Tucker Carlson: This is one of the most important stories of our time
This is one of the world's blackest paints
This is One of The Funkiest Bass Techniques There Is! (L#113)
No.1 Toxicologist: These Products Were Making Me Infertile And Are Harming Your Future Kids!
This Is One of the Best Reactions Ever to Winning 'Make It Rain'
THIS is one of the BEST hard rock performances I've ever seen! Enter Rick Derringer!
This is one of the COOLEST apps I've seen 👀 | App Review
Exclusive insights from A MINECRAFT MOVIE | Only in Theaters
'This is one of the best things I think I've EVER seen.' | Britain's Got Talent
Liam Payne's Funeral: One Direction Reunites
This is one of the happiest transformations we've ever seen! rescued abandoned puppy
This is One of the World’s Greatest Roads...(The Großglockner)
This is One of The Best Modern Lexus Models EVER Made!
Why The Wire is one of the Most Brilliant TV Shows Ever
Комментарии
 0:14:00
0:14:00
 0:04:07
0:04:07
 0:04:05
0:04:05
 0:00:59
0:00:59
 0:21:01
0:21:01
 0:01:00
0:01:00
 0:08:30
0:08:30
 0:00:49
0:00:49
 0:02:31
0:02:31
 0:00:31
0:00:31
 0:05:39
0:05:39
 0:00:42
0:00:42
 0:15:09
0:15:09
 1:59:40
1:59:40
 0:04:10
0:04:10
 0:21:46
0:21:46
 0:22:23
0:22:23
 0:03:07
0:03:07
 0:03:14
0:03:14
 0:01:47
0:01:47
 0:09:19
0:09:19
 0:08:06
0:08:06
 0:45:10
0:45:10
 0:18:43
0:18:43